3.1 Revisión del modelo de análisis de la varianza univariante ANOVA
En el modelo de análisis de la varianza univariante, disponemos de \(k\) muestras independientes que provienen de poblaciones normales con la misma varianza (modelo homocedástico). Es decir,
\[\begin{array}{cccccc} y_{11} & y_{12} & \cdots & y_{1\,n_1} & \mbox{de una población} & N\left(\mu_1,\sigma^2\right), \\ y_{21} & y_{22} & \cdots & y_{2\,n_2} & \mbox{de una población} & N\left(\mu_2,\sigma^2\right), \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ y_{k1} & y_{k2} & \cdots & y_{k\,n_k} &\mbox{de una población} & N\left(\mu_k,\sigma^2\right). \end{array}\]
Cada una de las \(k\) muestras (también denominadas grupos) está formada por variables independientes y con la misma distribución. Se supone además que las \(k\) muestras son independientes entre sí. Los grupos pueden corresponder, por ejemplo, a diferentes tratamientos aplicados por el investigador en un experimento. El primer objetivo de un modelo de análisis de la varianza es contrastar la hipótesis nula de que todas las medias son iguales. Planteamos así el contraste:
\[H_0: \mu_1=\mu_2=\cdots=\mu_k.\]
Ejemplo. En el trabajo clásico de Andrews and Herzberg (1985), se
comparan manzanos sobre seis tipos de portainjertos. En concreto, se
analizan ocho manzanos sobre cada tipo de portainjerto. Para cada
manzano se determina la circunferencia del tronco (mm \(\times\) 100) a
los 4 años. Los datos se encuentran en el fichero tronco.txt.
> tronco <- read.table("data/tronco.txt", header = TRUE)
> head(tronco)
portainjerto cir4
1 1 1.11
2 1 1.19
3 1 1.09
4 1 1.25
5 1 1.11
6 1 1.08En este caso \(k=6\) (tipos de portainjertos) y \(n_i=8\) para \(i=1,\ldots,6\) (número de árboles para cada tipo de portainjerto). El objetivo es determinar si existen diferencias significativas en el crecimiento de los manzanos debidas al tipo de portainjerto, ver Figura 3.1
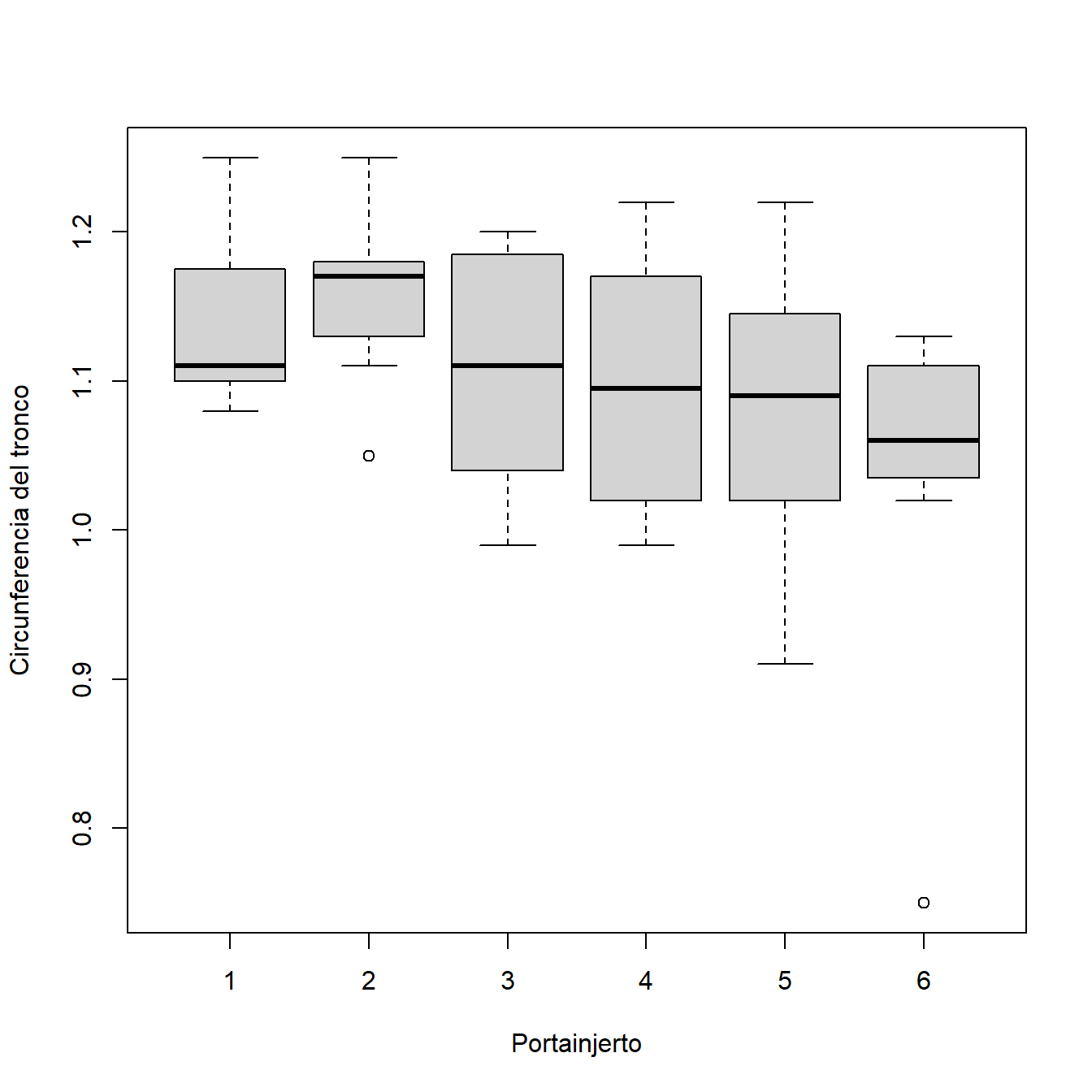
Figura 3.1: Boxplot para la circunferencia de tronco a los 4 años en cada tipo de portainjerto.
Denotamos mediante \(\overline{y}_{i\bullet}\) a la media muestral procedente de la población \(i\)-ésima, es decir,
\[\overline{y}_{i\bullet}=\frac{1}{n_i}\sum_{j=1}^{n_i} y_{ij}\] para \(i=1,\ldots,k\). Sea \(n=n_1+\ldots+n_k\) el número total de datos. Entonces, la media global de la muestra se calcula como:
\[\overline{y}_{\bullet\bullet} =\frac{1}{n}\sum_{i=1}^k \sum_{j=1}^{n_i} y_{ij}.\]
Se puede expresar el modelo de análisis multivariante de la varianza como un caso particular del modelo de regresión lineal. El modelo para cada observación es:
\[y_{ij}=\mu+\alpha_i+\epsilon_{ij}=\mu_i+\epsilon_{ij}\] con \(i=1,\ldots,k\) y \(j=1,\ldots, n_i\). En el modelo, \(\mu_i=\mu+\alpha_i\) es la media de la población \(i\)-ésima.
Queremos comparar las medias muestrales \(\overline{y}_{i\bullet}\) para ver si son suficientemente distintas como para llevarnos a pensar que las medias de cada población difieren. Para determinar si hay diferencias significativas entre las respuestas medias a distintos niveles del factor, el ANOVA descompone la variabilidad total. La variabilidad total, medida a través de la desviación cuadrática de los datos a la media global, admite la siguiente descomposición:
\[\sum_{i=1}^k \sum_{j=1}^{n_i} \left( y_{ij} - \overline y_{\bullet\bullet}\right)^2 =\sum_{i=1}^k \sum_{j=1}^{n_i} \left( y_{ij} - \overline{y}_{i\bullet} \right)^2 + \sum_{i=1}^k \sum_{j=1}^{n_i} \left( \overline{y}_{i\bullet} - \overline y_{\bullet\bullet} \right)^2.\]
Al igual que en regresión, lo representamos mediante la tabla de análisis de la varianza.
| Fuente de variación | Suma de cuadrados | Grados de libertad |
|---|---|---|
| Entre poblaciones (VE) | \({\sum_{i=1}^k {n_i} \left(\bar y_{i\bullet}-\bar y_{\bullet\bullet}\right)^2}\) | \(k-1\) |
| Error (VNE) | \({\sum_{i=1}^k \sum_{j=1}^{n_i} \left( y_{ij}-\bar y_{i\bullet}\right)^2}\) | \(n-k\) |
| Total (VT) | \({\sum_{i=1}^k \sum_{j=1}^{n_i} \left( y_{ij}-\bar y_{\bullet\bullet}\right)^2}\) | \(n-1\) |
Nos fijamos en que VE representa las desviaciones de las medias muestrales de cada población respecto a la media global. Sirve por lo tanto como medición de la variabilidad entre poblaciones (inter-grupos). Además, VNE representa las desviaciones de cada dato respecto a la media muestral de la población de la que procede. Es útil como medida de la variabilidad interna (intra-grupos), presente entre los individuos de la misma población. Para efectuar el contraste de igualdad de las medias debemos considerar un estadístico que mida la discrepancia respecto a la hipótesis nula de igualdad. Si las medias fueran iguales, las desviaciones entre poblaciones no deberían ser muy grandes, comparadas con las desviaciones dentro de cada población. Un estadístico razonable para el contraste es
\[F=\frac{VE/(k-1)}{{VNE}/(n-k)}=\frac{\sum_{i=1}^k \sum_{j=1}^{n_i} \left(\bar y_{i\bullet}-\bar y_{\bullet\bullet}\right)^2/(k-1)} {\sum_{i=1}^k \sum_{j=1}^{n_i} \left( y_{ij}-\bar y_{i\bullet}\right)^2/(n-k)}.\] Si la hipótesis nula \(H_0: \mu_1=\mu_2=\cdots=\mu_k\) es cierta, \(F\) presenta una distribución \(F\) de Snédecor \(F\in F_{(k-1),(n-k)}\). Rechazaremos \(H_0\) cuando para valores grandes de \(F\).
Ejemplo. Volvemos sobre el ejemplo de manzanos sobre diferentes tipos de portainjertos. Existen distintas formas de realizar un ANOVA en R. Esta es una de ellas:
> x <- factor(tronco[, 1])
> y <- tronco[, 2]
> z <- lm(y ~ x)
> anova(z)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 5 0.07356 0.0147121 1.931 0.1094
Residuals 42 0.31999 0.0076187 Vemos que el \(p\)-valor indica que no hay evidencias significativas para rechazar la hipótesis nula de igualdad de medias.