2.3 Contrastes sobre el vector de medias

$ \newcommand{\bm}[1]{\boldsymbol{#1}} $ $ \newcommand{\textnormal}[1]{\textrm{#1}} $

2.3 Contrastes sobre el vector de medias

A continuación veremos cómo se puede usar el test de razón de verosimilitudes para hacer inferencia en poblaciones normales multivariantes. En esta sección ilustraremos el caso del problema de inferencia sobre el vector de medias cuando la matriz de covarianzas es conocida, y también cuando es desconocida.

2.3.1 Contraste sobre el vector de medias con matriz de covarianzas conocida

En este apartado veremos como llevar a cabo un contraste sobre el vector de medias de una población normal asumiendo que la matriz de covarianzas $\bm\Sigma$ es conocida. Antes, repasaremos la teoría en el caso unidimensional.

2.3.1.1 Revisión del caso unidimensional $H_0:\mu=\mu_0$ con $\sigma^2$ conocida

La hipótesis de interés es que la media $\mu$ de una variable aleatoria $x$ es igual a un valor dado $\mu_0$ frente a la alternativa de que no es igual a $\mu_0$, es decir \[H_0:\mu=\mu_0\textnormal{ frente a }H_1:\mu\neq\mu_0.\] Dada una muestra $x_1,\ldots,x_n$ de normales $N(\mu,\sigma^2)$ con $\sigma^2$ conocida, se calcula la media muestral $\overline{x}$ y se compara con $\mu_0$ a través del estadístico

\[z=\frac{\overline{x}-\mu_0}{\sigma/\sqrt{n}}\]

que, bajo la hipótesis nula, se distribuye como una normal estándar. Por lo tanto, para un nivel de significación $\alpha=0.05$ rechazamos la hipótesis nula si $\left|z\right|\geq 1.96$. Equivalentemente

\[z^2=n(\overline{x}-\mu_0)\frac{1}{\sigma^2}(\overline{x}-\mu_0)\] y podríamos utilizar que $z^2$ se distribuye, bajo la hipótesis nula, como una ji-cuadrado con un grado de libertad. Entonces rechazaríamos $H_0$ si $z^2\geq 3.84$.

2.3.1.2 Contraste multivariante $H_0:\bm\mu=\bm{\mu_0}$ con $\bm\Sigma$ conocida

Partimos ahora de una muestra aleatoria simple $\bm{x_1},\ldots,\bm{x_n}\in N_d(\bm{\mu},\bm\Sigma)$ de vectores aleatorios independientes y con la misma distribución normal multivariante.

Suponiendo que la matriz de covarianzas $\bm\Sigma$ es conocida, deseamos llevar a cabo tareas de inferencia relativas al vector de medias $\bm{\mu}$. En concreto, podemos estar interesados en una región de confianza para $\bm{\mu}$, o podemos querer contrastar una hipótesis nula del tipo $H_0:\bm{\mu}=\bm{\mu_0}$.

Centrándonos en el contraste de la hipótesis nula $H_0:\bm{\mu}=\bm{\mu_0}$, vamos a abordar este problema mediante el procedimiento de razón de verosimilitudes. En esta situación, el estadístico de contraste sería:

\[-2\log \lambda(\bm{x})=-2\log \frac{L(\bm{x},\bm{\mu_0},\bm\Sigma)}{\sup_{\bm{\mu}} L(\bm{x},\bm{\mu},\bm\Sigma)}\] donde la función de verosimilitud es la que se ha tratado en la sección anterior.

De lo allí expuesto extraemos que, bajo la hipótesis nula, $H_0: \bm{\mu}=\bm{\mu_0}$, la función de log-verosimilitud adopta la forma:

\[\log L(\bm{x},\bm{\mu_0},\bm\Sigma) = c - \frac{n}{2} \log |\bm\Sigma | -\frac{1}{2} \sum_{i=1}^n \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right) -\frac{n}{2} \left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right)\] mientras que bajo la alternativa, aplicando la expresión (2.1), se tiene

\[\sup_{\bm{\mu}}\log L(\bm{x},\bm{\mu},\bm\Sigma) = c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \sum_{i=1}^n \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right).\]

En definitiva, el estadístico de contraste resulta:

\[-2\log \lambda(\bm{x})=-2\log \frac{L(\bm{x},\bm{\mu_0},\bm\Sigma)}{\sup_{\bm{\mu}} L(\bm{x},\bm{\mu},\bm\Sigma)} =n\left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right).\]

Observamos que si $H_0:\bm{\mu}=\bm{\mu_0}$ es cierta,

\[\overline{\bm{x}}\in N_d\left(\bm{\mu_0},\bm\Sigma/n\right)\] y, en consecuencia,

\[n\left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right)\in\chi_d^2.\]

Así, rechazaremos la hipótesis nula $H_0:\bm{\mu}=\bm{\mu_0}$ cuando

\[\label{testchi} n\left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right)>\chi_{d,\alpha}^2\] siendo $\chi_{d,\alpha}^2$ el cuantil $1-\alpha$ de la distribución $\chi_d^2$. La región de rechazo se corresponde con el exterior de un elipsoide en $\mathbb{R}^d$.

Ejemplo. Volvemos al estudio sobre Psicología educativa. Se le han realizado los dos tests de inteligencia a 20 alumnos de un centro universitario. La nota media obtenida por los 20 alumnos en el test de valoración de habilidades aritméticas fue de $102$ puntos. La nota media en el test de habilidades de memoria fue de $98$ puntos. Asumamos además que las notas obtenidas provienen de una distribución normal bivariante $N_2(\bm{\mu}, \bm\Sigma)$ siendo

\[\bm\Sigma=\left(\begin{array}{cc} 49 & 35 \\ 35 & 52 \end{array}\right).\] Queremos contrastar si las notas medias de estudiantes universitarios en los dos tests de inteligencia son iguales a 100. Es decir, queremos contrastar la hipótesis nula $H_0:\bm{\mu}=\bm{\mu_0}$, siendo $\bm{\mu_0}=(100,100)^\prime{}$.

A partir de la muestra obtenemos que $\overline{\bm{x}}=(\overline{x_1},\overline{x_2})^\prime{}=(102,98)^\prime{}$. Calculamos el valor del estadístico para el contraste multivariante.

\[n\left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right)=20\left(2,-2\right)\left(\begin{array}{cc} 49 & 35 \\ 35 & 52 \end{array}\right)^{-1} \left(\begin{array}{r} 2 \\ -2 \end{array}\right)=10.34014.\]

> Sigma <- matrix(c(49, 35, 35, 52), nrow = 2)
> xbar <- c(102, 98)
> mu0 <- c(100, 100)
> estad <- 20 * (xbar - mu0) %*% solve(Sigma) %*% (xbar - mu0)
> estad
         [,1]
[1,] 10.34014

Rechazamos la hipótesis nula (para un nivel de significación $\alpha=0.05$) ya que el valor del estadístico es mayor que $\chi_{d,\alpha}^2=5.991465$. También podemos calcular el $p$-valor del estadístico y razonar a partir de él (como el $p$-valor es menor que $\alpha=0.05$ se rechaza $H_0$ para dicho nivel de significación).

> alpha <- 0.05
> qchisq(1 - alpha, 2)
[1] 5.991465

> pvalue <- 1 - pchisq(estad, 2)
> pvalue
            [,1]
[1,] 0.005684182

Sin embargo, si planteamos los contrastes individuales $H_0:\mu_1=100$ y $H_0:\mu_2=100$ se tiene que

\[\frac{\overline{x_1}-\mu_0}{\sigma_1/\sqrt{n}}=\frac{102-100}{\sqrt{49/20}}=1.2777\] y

\[\frac{\overline{x_2}-\mu_0}{\sigma_2/\sqrt{n}}=\frac{98-100}{\sqrt{52/20}}= -1.24034.\] En ambos casos, el valor absoluto del estadístico es menor que 1.96 y por lo tanto no se rechazaría la hipótesis nula para ninguno de los dos contrastes individuales. En la Figura 2.4 se representan las zonas de rechazo y no rechazo para los contrastes univariantes y para el contraste bivariante correspondiente a los datos de este ejemplo ($n=20$). Si $\overline{\bm{x}}$ pertenece a la zona verde, no se rechaza la hipótesis nula $H_0:\bm\mu=\bm{\mu_0}$ siendo $\bm{\mu_0}=(100,100)^\prime$. Si $\overline{\bm{x}}$ pertenece a la zona azul, no se rechaza ni $H_0:\mu_1=100$ ni $H_0:\mu_2=100$. Fíjate que el punto $\overline{\bm{x}}=(\overline{x_1},\overline{x_2})^\prime{}=(102,98)^\prime{}$ está fuera de la elipse que representa la zona de no rechazo del test multivariante y sin embargo, cae en la zona de no rechazo de los dos contrastes univariantes.

$Zonas de rechazo y no rechazo para los contrastes univariantes y para el contraste bivariante correspondiente a los datos de tests de inteligencia ($n=20$). Si $\overline{\bm{x}}$ pertenece a la zona verde, no se rechaza la hipótesis nula $H_0:\bm\mu=\bm{\mu_0}$ siendo $\bm{\mu_0}=(100,100)^\prime$. Si $\overline{\bm{x}}$ pertenece a la zona azul, no se rechaza ni $H_0:\mu_1=100$ ni $H_0:\mu_2=100$.$

Figura 2.4: Zonas de rechazo y no rechazo para los contrastes univariantes y para el contraste bivariante correspondiente a los datos de tests de inteligencia ($n=20$). Si $\overline{\bm{x}}$ pertenece a la zona verde, no se rechaza la hipótesis nula $H_0:\bm\mu=\bm{\mu_0}$ siendo $\bm{\mu_0}=(100,100)^\prime$. Si $\overline{\bm{x}}$ pertenece a la zona azul, no se rechaza ni $H_0:\mu_1=100$ ni $H_0:\mu_2=100$.

2.3.2 Contraste sobre el vector de medias con matriz de covarianzas desconocida

Veremos ahora como llevar a cabo un contraste sobre el vector de medias de una población normal asumiendo que la matriz de covarianzas $\bm\Sigma$ es desconocida. Repasaremos de nuevo en primer lugar la teoría en el caso unidimensional.

2.3.2.1 Revisión del caso unidimensional $H_0:\mu=\mu_0$ con $\sigma^2$ desconocida

La hipótesis de interés es que la media $\mu$ de una variable aleatoria $x$ es igual a un valor dado $\mu_0$ frente a la alternativa de que no es igual a $\mu_0$, es decir

\[H_0:\mu=\mu_0\textnormal{ frente a }H_1:\mu\neq\mu_0.\] Dada una muestra $x_1,\ldots,x_n$ de normales $N(\mu,\sigma^2)$ con $\sigma^2$ desconocida, se calcula la media muestral $\overline{x}$ y se compara con $\mu_0$ a través del estadístico

\[t=\frac{\overline{x}-\mu_0}{s_c/\sqrt{n}}\] siendo $s_c=\sum_{i=1}^n(x_i-\overline{x})^2/(n-1)$ la cuasivarianza muestral. Bajo la hipótesis nula, el estadístico se distribuye como una $t$ de Student con $n-1$ grados de libertad. Por lo tanto, para un nivel de significación $\alpha$ rechazamos la hipótesis nula si $\left|t\right|\geq t_{\alpha/2}$, siendo $t_{\alpha/2}$ el cuantil $1-\alpha/2$ de la distribución $t$ de Student con $n-1$ grados de libertad. Equivalentemente

\[\begin{equation} t^2=n(\overline{x}-\mu_0)\frac{1}{s_c^2}(\overline{x}-\mu_0). \tag{2.2} \end{equation}\]

Veremos que esta forma de escribir el estadístico estará relacionada con la versión multivariante del contraste.

2.3.2.2 Contraste multivariante $H_0:\bm\mu=\bm{\mu_0}$ con $\bm\Sigma$ desconocida

Disponemos ahora de una muestra aleatoria simple $\bm{x_1},\ldots,\bm{x_n}\in N_d(\bm{\bm{\mu}},\bm\Sigma)$ y deseamos realizar tareas de inferencia relativas al vector de medias $\bm{\mu}$. Suponemos que la matriz de covarianzas $\bm\Sigma$ es desconocida.

El estadístico de razón de verosimilitudes para el contraste de la hipótesis nula $H_0:\bm{\mu}=\bm{\mu_0}$ sería:

\[-2\log \lambda(\bm{x}) =-2\log \frac{\sup_{\bm\Sigma} L(\bm{x},\bm{\mu_0},\bm\Sigma)}{\sup_{\bm{\mu},\bm\Sigma} L(\bm{x},\bm{\mu},\bm\Sigma)}.\]

Nótese que ahora, al ser $\bm\Sigma$ desconocida, se convierte en un parámetro tanto bajo la hipótesis nula como bajo la alternativa, parámetro que será estimado por máxima verosimilitud.

Bajo la alternativa, hemos visto en la sección anterior que los estimadores de máxima verosimilitud del vector de medias y la matriz de covarianzas (sin restricciones) son $\overline{\bm{x}}$ y $\bm{S}$, respectivamente. Asimismo, la función de verosimilitud tiene como máximo:

\[\sup_{\bm\Sigma}\sup_{\bm{\mu}}\log L(\bm{x},\bm{\mu},\bm\Sigma) = c - \frac{n}{2} \left( \log |\bm{S}| + \mbox{traza} \left( \bm{S}^{-1} \bm{S} \right)\right) = c - \frac{n}{2} \left( \log |\bm{S}| + d\right).\]

A continuación maximizamos la verosimilitud bajo la hipótesis nula. Para ello basta con expresar la verosimilitud en una forma similar a la anterior:

\[\begin{aligned} \log L(\bm{x},\bm{\mu_0},\bm\Sigma) &= c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \mbox{traza} \left[\sum_{i=1}^n \left(\bm{x_i}-\bm{\mu_0}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\bm{\mu_0}\right)\right] \\ &= c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \sum_{i=1}^n \mbox{traza} \left[ \bm\Sigma^{-1} \left(\bm{x_i}-\bm{\mu_0}\right) \left(\bm{x_i}-\bm{\mu_0}\right)^\prime{} \right] \\ &= c - \frac{n}{2} \left( \log |\bm\Sigma| + \mbox{traza} \left( \bm\Sigma^{-1} \hat{\bm\Sigma}_{\bm{\mu_0}} \right)\right)\end{aligned}\]

siendo $\hat{\bm\Sigma}_{\bm{\mu_0}}=\frac{1}{n}\sum_{i=1}^n \left(\bm{x_i}-\bm{\mu_0}\right) \left(\bm{x_i}-\bm{\mu_0}\right)^\prime{}$, el cual resulta ser un estimador razonable de la matriz de covarianzas bajo la hipótesis de que la media vale $\bm{\mu_0}$. Por lo demás los pasos son idénticos al caso anterior, salvo que se ha puesto $\bm{\mu_0}$ allí donde se hallaba $\overline{\bm{x}}$. Aplicando de nuevo el lema, concluimos que $\hat{\bm\Sigma}_{\bm{\mu_0}}$ es el estimador de máxima verosimilitud de la matriz de covarianzas bajo la hipótesis nula, y que la función de verosimilitud bajo dicha hipótesis alcanza el valor máximo:

\[\sup_{\bm\Sigma}\log L(\bm{x},\bm{\mu_0},\bm\Sigma) = c - \frac{n}{2} \left( \log |\hat{\bm\Sigma}_{\bm{\mu_0}}| + d \right).\]

Entonces el estadístico de contraste mediante la razón de verosimilitudes resulta:

\[-2\log \lambda(\bm{x}) =-2\log \frac{\sup_{\bm\Sigma} L(\bm{x},\bm{\mu_0},\bm\Sigma)}{\sup_{\bm{\mu},\bm\Sigma} L(\bm{x},\bm{\mu},\bm\Sigma)} =n\left( \log |\hat{\bm\Sigma}_{\bm{\mu_0}}| - \log |\bm{S}| \right).\]

Descomponemos

\[\begin{aligned} \hat{\bm\Sigma}_{\bm{\mu_0}} &= \frac{1}{n} \sum_{i=1}^n \left(\bm{x_i}-\bm{\mu_0}\right) \left(\bm{x_i}-\bm{\mu_0}\right)^\prime{} \\ &= \frac{1}{n} \sum_{i=1}^n \left[ \left(\bm{x_i}-\overline{\bm{x}}\right) \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{} + \left(\overline{\bm{x}}-\bm{\mu_0}\right) \left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{} + 2 \left(\overline{\bm{x}}-\bm{\mu_0}\right) \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{} \right] \\ &= \bm{S}+\bm{r}\bm{r}^\prime{}\end{aligned}\] siendo $\bm{r}=\overline{\bm{x}}-\bm{\mu_0}$. Sustituyendo en el estadístico de contraste obtenemos

\[\begin{aligned} -2\log \lambda(\bm{x}) &= n\left( \log |\bm{S}+\bm{r}\bm{r}^\prime{}| - \log |\bm{S}| \right) \\ &= n\left( \log \left(|\bm{S}|\cdot \left|\bm{I_d}+\bm{S}^{-1}\bm{r}\bm{r}^\prime{}\right|\right) - \log |\bm{S}| \right) \\ &=n \log \left|\bm{I_d}+\bm{S}^{-1}\bm{r}\bm{r}^\prime{}\right|.\end{aligned}\]

Estudiemos, pues, el determinante que aparece en el último término. En (a) denotamos mediante $\lambda_1,\ldots,\lambda_d$ a los autovalores de $\bm{S}^{-1}\bm{r}\bm{r}^\prime{}$, y observamos que $1+\lambda_1,\ldots,1+\lambda_d$ son los autovalores de $\bm{I_d}+\bm{S}^{-1}\bm{r}\bm{r}^\prime{}$. En (b) y (c) usamos que la matriz $\bm{S}^{-1}\bm{r}\bm{r}^\prime{}$ es de rango uno.

\[ \begin{aligned} \left|\bm{I_d}+\bm{S}^{-1}\bm{r}\bm{r}^\prime{}\right|&\stackrel{(a)}{=} \prod_{j=1}^d \left(1+\lambda_j\right)\\ &\stackrel{(b)}{=} 1+\lambda_1\\ &\stackrel{(c)}{=} 1+{\textnormal{traza}}\left(\bm{S}^{-1}\bm{r}\bm{r}^\prime{}\right)\\ &=1+{\textnormal{traza}}\left(\bm{r}^\prime{}\bm{S}^{-1}\bm{r}\right)\\ &=1+\bm{r}^\prime{}\bm{S}^{-1}\bm{r}. \end{aligned}\]

Finalmente,

\[-2\log \lambda(\bm{x})=n\log\left(1+\bm{r}^\prime{}\bm{S}^{-1}\bm{r}\right)\]

será el estadístico de contraste y rechazaremos la hipótesis nula si este estadístico toma un valor demasiado grande.

Será equivalente si consideramos el estadístico

\[\bm{r}^\prime{}\bm{S}^{-1}\bm{r}=\left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{} \bm{S}^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right)\]

y rechazamos la hipótesis nula cuando este nuevo estadístico toma un valor demasiado grande. Nótese que el estadístico anterior se obtiene tras aplicar una transformación creciente a este último.

El estadístico recuerda al comentado en (2.2) para el caso univariante si tenemos en cuenta que:

\[T^2=(n-1)\left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{} \bm{S}^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right)=n\left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{} \bm{S_c}^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right)\]

donde $\bm{S_c}=n/(n-1)\bm{S}$ denota la matriz de covarianzas corregida. La distribución de $T^2$ bajo la hipótesis nula fue obtenida por Hotelling (1936). Se tiene que, si $H_0$ es cierta, el estadístico $T^2$ sigue una distribución $\Gamma^2$ de Hotelling⁴ de parámetros $d$ y $n-1$. La distribución $\Gamma^2$ de Hotelling juega un papel semejante a la distribución $t$ de Student en el caso multivariante. Puedes encontrar propiedades y resultados sobre esta distribución en el Anexo A. Los valores críticos de la distribución $\Gamma^2$ de Hotelling están tabulados. Aun así, se puede convertir una variable con distribución $\Gamma^2$ de Hotelling en otra con distribución $F$ de Snédecor. De este modo se evita la necesidad de considerar nuevas tablas de cuantiles. Simplemente se efectuaría la transformación y se apelaría a las tablas y operaciones conocidas para la $F$ de Snédecor. En nuestro caso se tiene que, bajo $H_0$,

\[\frac{n-d}{d} \left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{} \bm{S}^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right) \in F_{d,n-d}.\]

En definitiva, rechazaremos la hipótesis nula $H_0: \bm{\mu}=\bm{\mu_0}$ si

\[\frac{n-d}{d} \left(\overline{\bm{x}}-\bm{\mu_0}\right)^\prime{} \bm{S}^{-1} \left(\overline{\bm{x}}-\bm{\mu_0}\right) > f_{d,n-d,\alpha}\] siendo $f_{d,n-d,\alpha}$ el cuantil $1-\alpha$ de la distribución $F_{d,n-d}$.

Ejemplo. El fichero notas.txt contiene las puntuaciones obtenidas por los 20 alumnos que han realizado los tests de inteligencia citados en los ejemplos previos. Asumamos ahora que las notas obtenidas provienen de una distribución normal bivariante $N_2(\bm{\mu}, \bm\Sigma)$ pero que $\bm\Sigma$ es desconocida. Queremos contrastar la hipótesis nula $H_0:\bm{\mu}=\bm{\mu_0}$, siendo $\bm{\mu_0}=(100,100)^\prime{}$.

> tests <- read.table("data/notas.txt", header = TRUE)
> n <- dim(tests)[1]
> d <- dim(tests)[2]
> xbar <- colMeans(tests)
> xbar
Test1 Test2 
  102    98

> S <- (n - 1)/n * cov(tests)
> S
      Test1 Test2
Test1  84.1  38.3
Test2  38.3  32.6

> mu0 <- c(100, 100)
> estad <- (n - d)/d * (xbar - mu0) %*% solve(S) %*% (xbar - mu0)
> estad
         [,1]
[1,] 5.458867

Rechazamos la hipótesis nula (para un nivel de significación $\alpha=0.05$) ya que el valor del estadístico es mayor que $f_{d,n-d,\alpha}=3.554557$. También podemos calcular el $p$-valor del estadístico y razonar a partir de él (como el $p$-valor es menor que $\alpha=0.05$ se rechaza $H_0$ para dicho nivel de significación).

> alpha <- 0.05
> qf(1 - alpha, d, n - d)
[1] 3.554557

> pvalue <- 1 - pf(estad, d, n - d)
> pvalue
          [,1]
[1,] 0.0140273

En la Figura 2.5 se representa en rojo la zona de no rechazo del contraste bivariante correspondiente a los datos de este ejemplo ($n=20$) en comparación con la zona de no rechazo cuando se suponía que la matriz de covarianzas era conocida (elipse en verde).

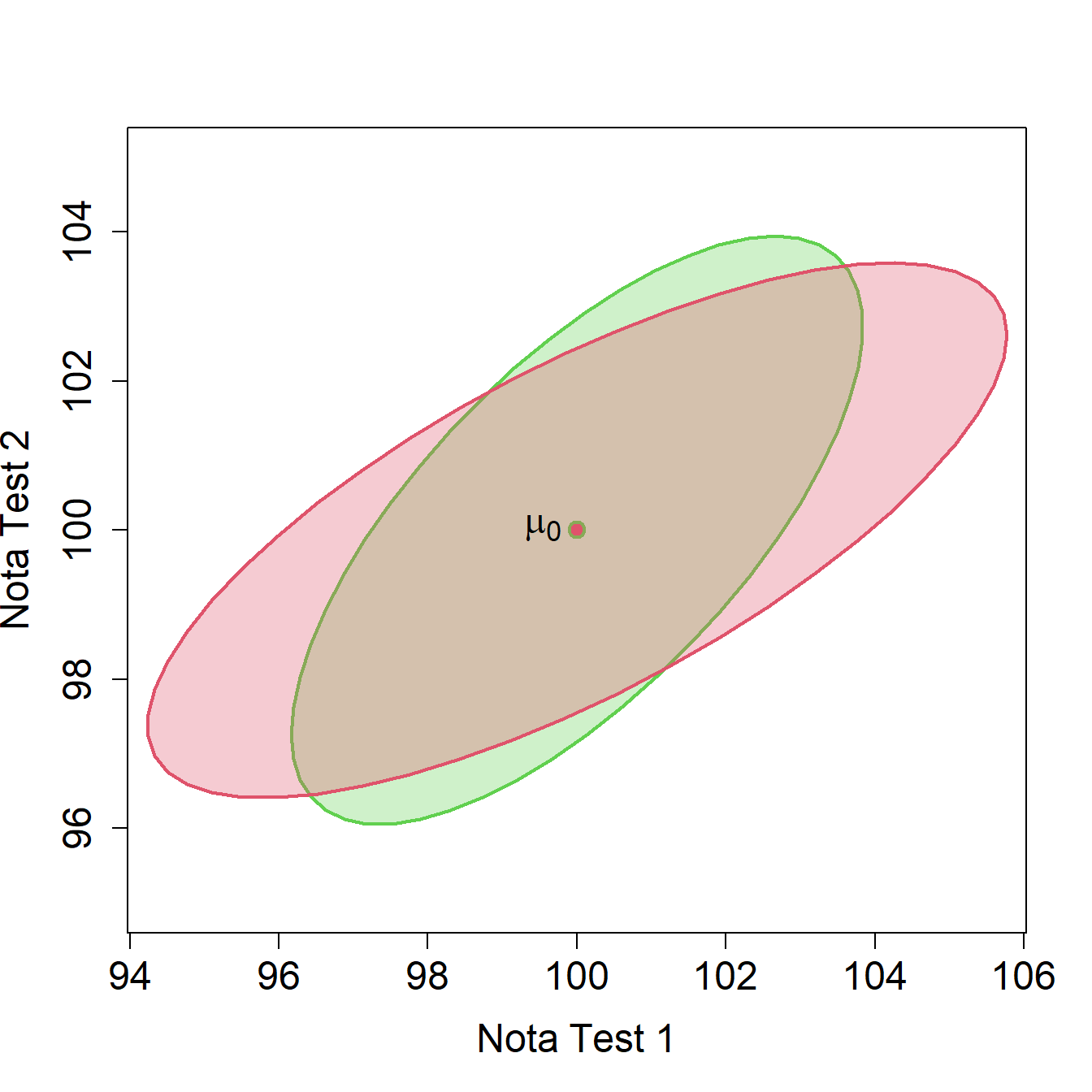
$Zonas de rechazo y no rechazo para el contraste bivariante correspondiente a los datos de tests de inteligencia ($n=20$). Para el caso en que se conoce la matriz de covarianzas, rechazamos la hipótesis nula si $\overline{\bm{x}}$ no pertenece a la elipse en verde. Para el caso en que se desconoce la matriz de covarianzas, rechazamos la hipótesis nula si $\overline{\bm{x}}$ no pertenece a la elipse en rojo.$

Figura 2.5: Zonas de rechazo y no rechazo para el contraste bivariante correspondiente a los datos de tests de inteligencia ($n=20$). Para el caso en que se conoce la matriz de covarianzas, rechazamos la hipótesis nula si $\overline{\bm{x}}$ no pertenece a la elipse en verde. Para el caso en que se desconoce la matriz de covarianzas, rechazamos la hipótesis nula si $\overline{\bm{x}}$ no pertenece a la elipse en rojo.

References

Hotelling, Harold. 1936. “Relations Between Two Sets of Variates.” Biometrika 28 (3/4): 321–77.

Formalmente, dadas $\bm{Z}\in N_d(\bm{0},\bm{I_d})$ y $\bm{R}\in W_d(\bm{I_d},m)$ independientes, con $m\geq d$ se dice que la variable aleatoria unidimensional $m\bm{Z}^{\prime} \bm{R}^{-1} \bm{Z} \in \Gamma^2(d,m)$ tiene una distribución $\Gamma^2$ de Hotelling de parámetros $d$ y $m$.↩︎