1.5 Distancias estadísticas
El concepto de distancia entre objetos o individuos observados permite interpretar geométricamente muchas técnicas de análisis multivariante. En el caso unidimensional, la distancia entre dos puntos \(x\) e \(y\) se mide de manera natural mediante la distancia euclídea \(\left|x-y\right|\).
Cuando disponemos de una variable vectorial, cada dato es un punto en \(\mathbb{R}^d\) y podríamos entonces pensar en utilizar de nuevo la distancia euclídea en el contexto multidimensional. A partir de ahora sean \(\bm{x_i}=(x_{i1},\ldots,x_{id})^\prime{}\) y \(\bm{x_k}=(x_{k1},\ldots,x_{kd})^\prime{}\) las observaciones de dos individuos \(i\), \(k\) obtenidas al medir el vector \(d\)-dimensional \((x_1,\ldots, x_d)^\prime{}\).
1.5.1 Distancia euclídea
Se define la distancia euclídea entre \(\bm{x_i}\) y \(\bm{x_k}\) como
\[d_E(\bm{x_i},\bm{x_k})=\sqrt{\sum_{j=1}^d{(x_{ij}-x_{kj})^2}}.\]
La distancia euclídea es la más utilizada pero tiene como inconvenientes que depende de las unidades de medida de las variables (no es invariante ante cambios de escala) y presupone que las variables son incorrelacionadas y de varianza unidad.
Ejemplo. Supongamos que disponemos de los datos de peso y estatura de 300 mujeres con edades comprendidas entre 30 y 40 años. Queremos determinar la posición con respecto a la media de tres nuevas mujeres a partir de sus respectivos pesos y estaturas. Supongamos que la mujer \(A\) pesa \(63\) kg. y mide \(180\) cm. La mujer \(B\) pesa \(60\) kg. y mide \(177\) cm. La mujer \(C\) pesa \(70\) kg. y mide \(177\) cm. Los datos se muestran en la Figura 1.6
Si bien parece evidente que la posición de las tres mujeres con respecto a la media es diferente (la mujer \(C\) parece más “cercana” a la media que la \(A\) y la \(B\)), la distancia euclídea de todos los puntos a la media es la misma.

Figura 1.6: Peso (en kg.) y estatura (en cm.) de 300 mujeres con edades comprendidas entre 30 y 40 años. En rojo se representa el peso medio y la estatura media. En azul, datos de las mujeres A, B y C.
1.5.2 Distancia euclídea estandarizada por columnas
Una manera de evitar el problema de que la distancia dependa de las unidades de medida de las variables, consiste en dividir cada variable por un término que elimine el efecto de la escala.
Se define la distancia euclídea estandarizada por columnas entre \(\bm{x_i}\) y \(\bm{x_k}\) como
\[d_{Est}(\bm{x_i},\bm{x_k})=\sqrt{\sum_{j=1}^d{\left(\frac{x_{ij}-x_{kj}}{\sigma_j}\right)^2}}.\] Su utilidad radica en que es una forma de determinar la similitud entre dos variables aleatorias multidimensionales invariante ante cambios de escala. Puede verse como una distancia euclídea donde cada coordenada se pondera inversamente proporcional a la varianza.
Tiene como inconvenientes que presupone que las variables son incorrelacionadas.
Ejemplo. En el ejemplo anterior de los datos de peso y estatura de 300 mujeres, la distancia euclídea estandarizada por columnas de la mujer \(A\) a la media es mayor que la distancia euclídea estandarizada por columnas de las mujeres \(B\) y \(C\) a la media. Aun así, la distancia euclídea estandarizada por columnas de las mujeres \(B\) y \(C\) a la media es la misma.
1.5.3 Distancia de Mahalanobis
Se define la distancia de Mahalanobis entre \(\bm{x_i}\) y \(\bm{x_k}\) como
\[d_M(\bm{x_i},\bm{x_k})=\sqrt{(\bm{x_i}-\bm{x_k})^\prime{}\bm\Sigma^{-1}(\bm{x_i}-\bm{x_k})}.\]
Geométricamente equivale a girar la nube de puntos hasta eliminar las correlaciones y luego calcular la distancia para los datos estandarizados. Es adecuada como medida de discrepancia entre datos, porque es invariante ante cambios de escala y tiene en cuenta las correlaciones entre las variables.
Además,
\(d_M\equiv d_E\) cuando \(\bm\Sigma=\bm{I_d}\).
\(d_M\equiv d_{Est}\) cuando \(\bm\Sigma=\textnormal{diag}(\sigma_1^2,\ldots,\sigma_d^2)\).
En caso de que la matriz de covarianzas sea desconocida se calcula
\[d_M(\bm{x_i},\bm{x_k})=\sqrt{(\bm{x_i}-\bm{x_k})^\prime{}\bm{S}^{-1}(\bm{x_i}-\bm{x_k})}.\]
Ejemplo. En el ejemplo anterior de los datos de peso y estatura de 300 mujeres, la distancia de Mahalanobis de la mujer \(A\) a la media es mayor que la distancia de Mahalanobis de la mujer \(B\) a la media, que a su vez es mayor que la distancia de Mahalanobis de la mujer \(C\) a la media.
1.5.4 Estandarización
Una transformación lineal que tiene un interés especial es la estandarización. La estandarización (o tipificación) de una variable aleatoria se consigue restando la media y dividiendo por la desviación típica (raíz cuadrada de la varianza). De esta manera se consigue que la nueva variable transformada tenga media cero y varianza uno.
En el caso de un vector aleatorio de dimensión \(d\), con \(d\) mayor que uno, podemos pensar en estandarizar cada una de sus variables. Como resultado de esta estandarización univariante se obtiene un vector cuyas componentes tienen todas media cero y desviación típica uno. Sin embargo, puede haber correlación entre las variables que componen el vector.
Ejemplo. En la Figura 1.7 se muestran dos diagramas de dispersión para los datos de peso y estatura de mujeres. El primero de ellos representa los datos tras haber estandarizado de manera univariante las dos variables. Esto hace que se hayan contraído los ejes. Se mantiene la correlación positiva, aunque la orientación de la nube de puntos ahora es más próxima a la diagonal, pues ambas variables tienen la misma dispersión.
El segundo gráfico muestra el diagrama de dispersión de los datos tras haberles aplicado una estandarización bivariante.
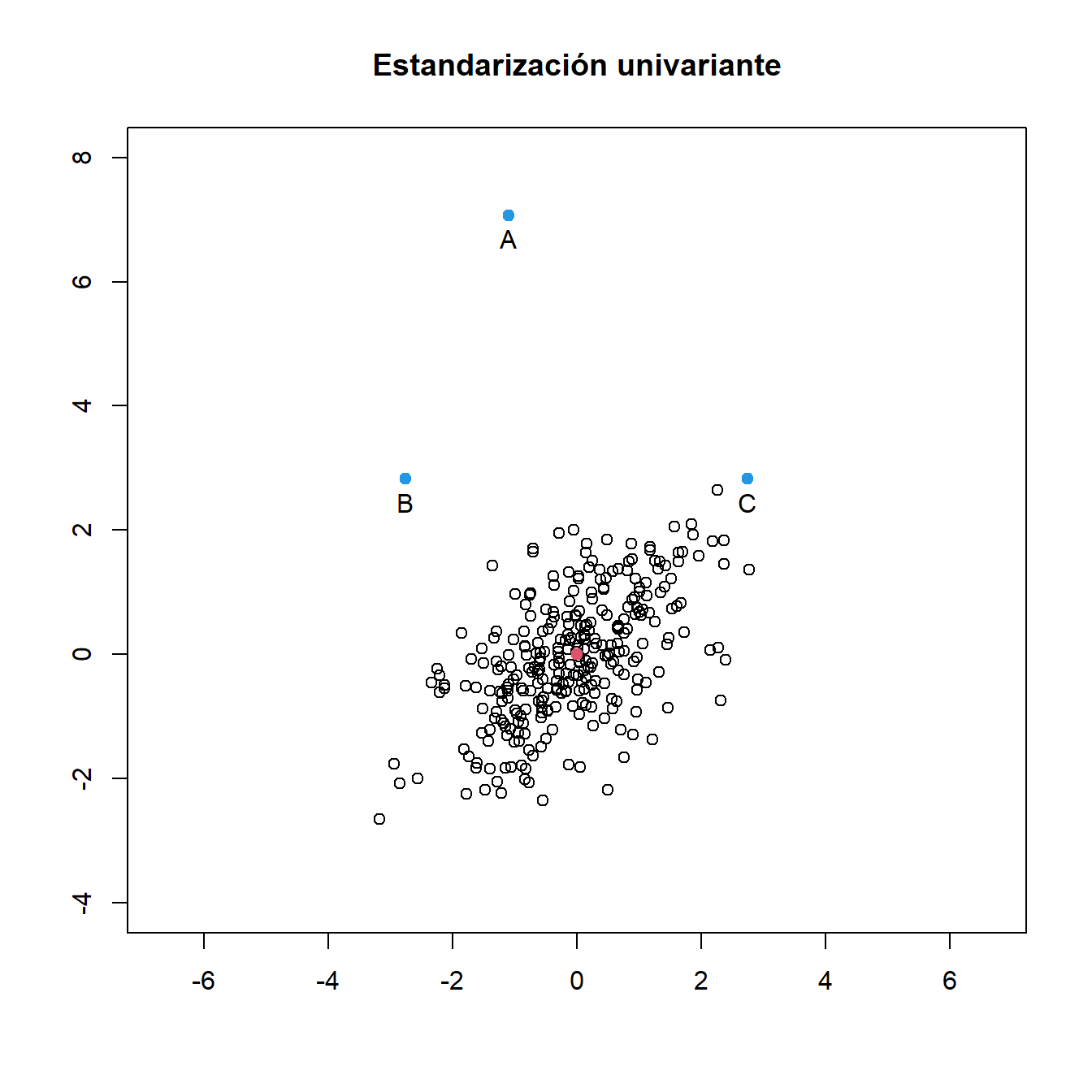
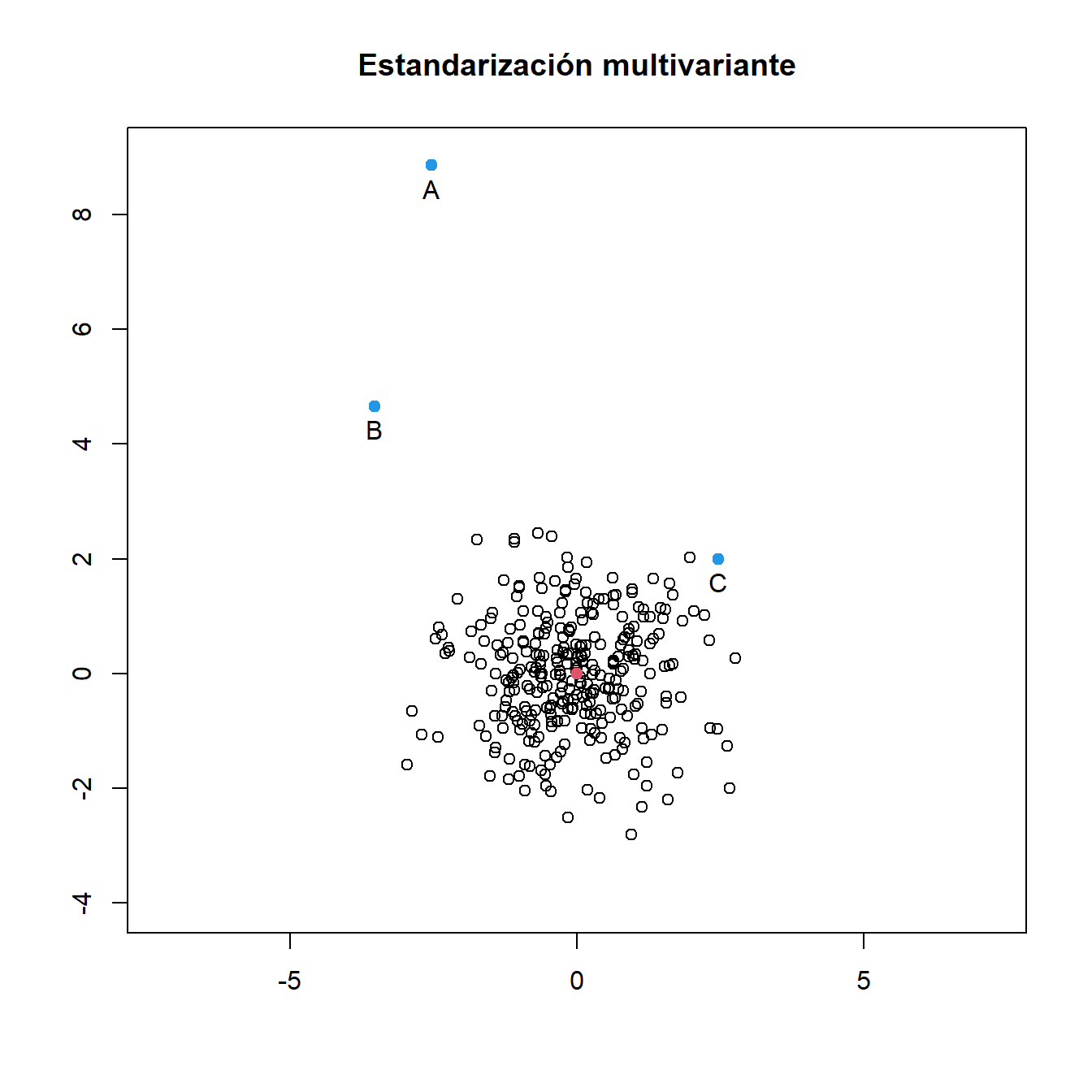
Figura 1.7: Estandarización univariante y multivariante
La estandarización multivariante se obtiene así:
\[\bm{y}=\bm{\Sigma^{-1/2}}(\bm{x}-\bm\mu)\] donde \(\bm\mu\) denota el vector de medias, \(\bm\Sigma\) es la matriz de covarianzas y \(\bm{\Sigma^{-1/2}}\) es una matriz \(d\times d\) que definiremos más adelante. Por las propiedades vistas en la sección anterior, se puede comprobar que:
El vector estandarizado tiene media cero:
\[E(\bm{y})=E(\bm{\Sigma^{-1/2}}(\bm{x}-\bm\mu))=\bm{\Sigma^{-1/2}}E(\bm{x}-\bm\mu)=0.\]
La matriz de covarianzas de \(\bm{y}\) es la matriz identidad \(d\times d\), \(\bm{I_d}\):
\[\mbox{Cov}(\bm{y},\bm{y})=\mbox{Cov}(\bm{\Sigma^{-1/2}}(\bm{x}-\bm\mu),\bm{\Sigma^{-1/2}}(\bm{x}-\bm\mu))=\bm{\Sigma^{-1/2}}\mbox{Cov}(\bm{x},\bm{x})(\bm{\Sigma^{-1/2}})^\prime{} \stackrel{(a)}{=}\bm{I_d}.\]
Para obtener la matriz \(\bm{\Sigma^{-1/2}}\), de manera que se cumpla la igualdad (a) en el cálculo anterior de la matriz de covarianzas, tendremos presente que toda matriz de covarianzas es una matriz simétrica y semidefinida positiva. Así, se le puede aplicar la descomposición en autovalores y autovectores, que vemos a continuación.
Si \(\bm{A}\) es una matriz simétrica, entonces
\[\bm{A}=\left(\bm{v_1},\ldots,\bm{v_d}\right)\left(\begin{array}{ccc} \lambda_1 & & 0 \\ & \ddots & \\ 0 & & \lambda_d \end{array}\right)\left(\begin{array}{c} \bm{v_1}^{\prime} \\ \vdots \\ \bm{v_d}^{\prime} \end{array}\right)\] siendo \(\bm{v_1},\ldots,\bm{v_d}\) una base ortonormal de autovectores de \(\bm{A}\) y \(\lambda_1,\ldots,\lambda_d\) sus autovalores asociados. \(\bm{A}\) se dice definida positiva si todos los autovalores de \(\bm{A}\) son positivos. En ese caso se puede emplear para definir una norma (y una distancia): \(\|\bm{x}\|^2=\bm{x}'\bm{A}\bm{x}\).
Entonces, se puede obtener \(\bm{\Sigma^{-1/2}}\) a partir de los autovalores y autovectores de \(\bm\Sigma\), de la siguiente manera:
\[{\bm{\Sigma^{-1/2}}}=\left(\bm{v_1},\ldots,\bm{v_d}\right)\left(\begin{array}{ccc} 1/\sqrt{\lambda_1} & & 0 \\ & \ddots & \\ 0 & & 1/\sqrt{\lambda_d} \end{array}\right)\left(\begin{array}{c} \bm{v_1}^{\prime} \\ \vdots \\ \bm{v_d}^{\prime} \end{array}\right).\]