4.2 Propiedades geométricas de las componentes principales
Esta sección contiene dos propiedades geométricas interesantes, que cumplen las componentes principales, cuando se comparan con el modelo de regresión. En primer lugar veremos que las componentes principales también son aproximaciones mínimo-cuadráticas del vector aleatorio, y en segundo lugar veremos que en el caso de un vector bivariante \(\bm{x}=(x_1,x_2)^\prime{}\), la primera componente principal describe una recta que pasa entre las dos rectas de regresión lineal simple, una de \(x_2\) sobre \(x_1\) y la otra de \(x_1\) sobre \(x_2\).
4.2.1 Las componentes principales como mejores aproximaciones mínimo-cuadráticas
Recordemos que la componente principal es la variable aleatoria unidimensional \(z_1=\bm{v_1}^{\prime} \bm{x}\). Al proyectar el vector \(\bm{x}\) sobre la recta que pasa por el origen con la dirección \(\bm{v_1}\), se obtiene el vector aleatorio
\[\bm{z_1^m}=\bm{v_1} z_1=\bm{v_1} \bm{v_1}^{\prime} \bm{x}\] que coincide con la representación de la primera componente \(z_1\) en \({\Bbb R}^d\) a lo largo de la dirección \(\bm{v_1}\).
Observamos que este vector aleatorio está contenido en un espacio de dimensión uno. De hecho, su matriz de covarianzas es
\[\textnormal{Cov}(\bm{z_1^m},\bm{z_1^m})=\textnormal{Cov}(\bm{v_1} z_1, \bm{v_1} z_1)=\bm{v_1} \textnormal{Cov}(z_1,z_1) \bm{v_1}^{\prime}= \textnormal{Var}(z_1) \bm{v_1} \bm{v_1}^{\prime} =\lambda_1 \bm{v_1} \bm{v_1}^{\prime}\] la cual claramente es una matriz de rango uno y no es más que el primer sumando de la descomposición espectral de \(\bm\Sigma\).
Centramos el vector \(\bm{z_1^m}\) en el vector de medias de \(\bm{x}\), \(\bm\mu=E(\bm{x})\).
\[\bm{z_1^{mc}}=\bm{z_1^m}-E(\bm{z_1^m})+E(\bm{x})=\bm\mu + \bm{v_1} z_1^c\] siendo \(z_1^c=\bm{v_1}^{\prime} (\bm{x}-\bm\mu)\) la primera componente centrada.
Este vector aleatorio \(\bm{z_1^{mc}}\) es el resultado de proyectar el vector \(\bm{x}\) sobre la recta que pasa por el vector de medias \(\bm\mu\) y tiene dirección \(\bm{v_1}\).
Teorema 4.4 La recta que pasa por el vector de medias \(\bm\mu=E(\bm{x})\) y tiene dirección \(\bm{v_1}\) es la que hace mínima la distancia cuadrática del vector aleatorio \(\bm{x}\) a la recta, definiendo esta distancia cuadrática como la media del cuadrado de la distancia euclídea usual (distancia ortogonal o menor distancia) del vector aleatorio \(\bm{x}\) a la recta.
Observación. Este resultado debe relacionarse con la recta de regresión, que hace mínima la media (suma en el caso de una muestra) de la distancia vertical a la recta. En este caso consideramos la distancia ortogonal (la menor distancia), pues no hay variable respuesta ni variable explicativa, sino que todas las variables son tratadas de igual modo.
4.2.2 Posición en el plano de la 1ª componente principal respecto a las rectas de regresión
Sea \((x,y)\) un vector aleatorio en el plano. Se puede demostrar que al representar en el plano \(XY\) la primera componente principal, junto con las dos rectas de regresión de \(y\) sobre \(x\) y de \(x\) sobre \(y\), obtenemos tres rectas que pasan por el vector de medias, y la primera componente principal forma una recta “menos horizontal” que la recta de regresión de \(y\) sobre \(x\), pero "más horizontal" que la recta de regresión de \(x\) sobre \(y\).
Ejemplo. Se ha obtenido la muestra siguiente de un vector aleatorio \((x,y)\): (-3,7), (1,4), (0,6), (3,5), (1,9), (7,7), (6,9), (8,10), (7,12), (10,11). Representamos en la Figura 4.4 el diagrama de dispersión, junto con la primera componente principal y las dos rectas de regresión.
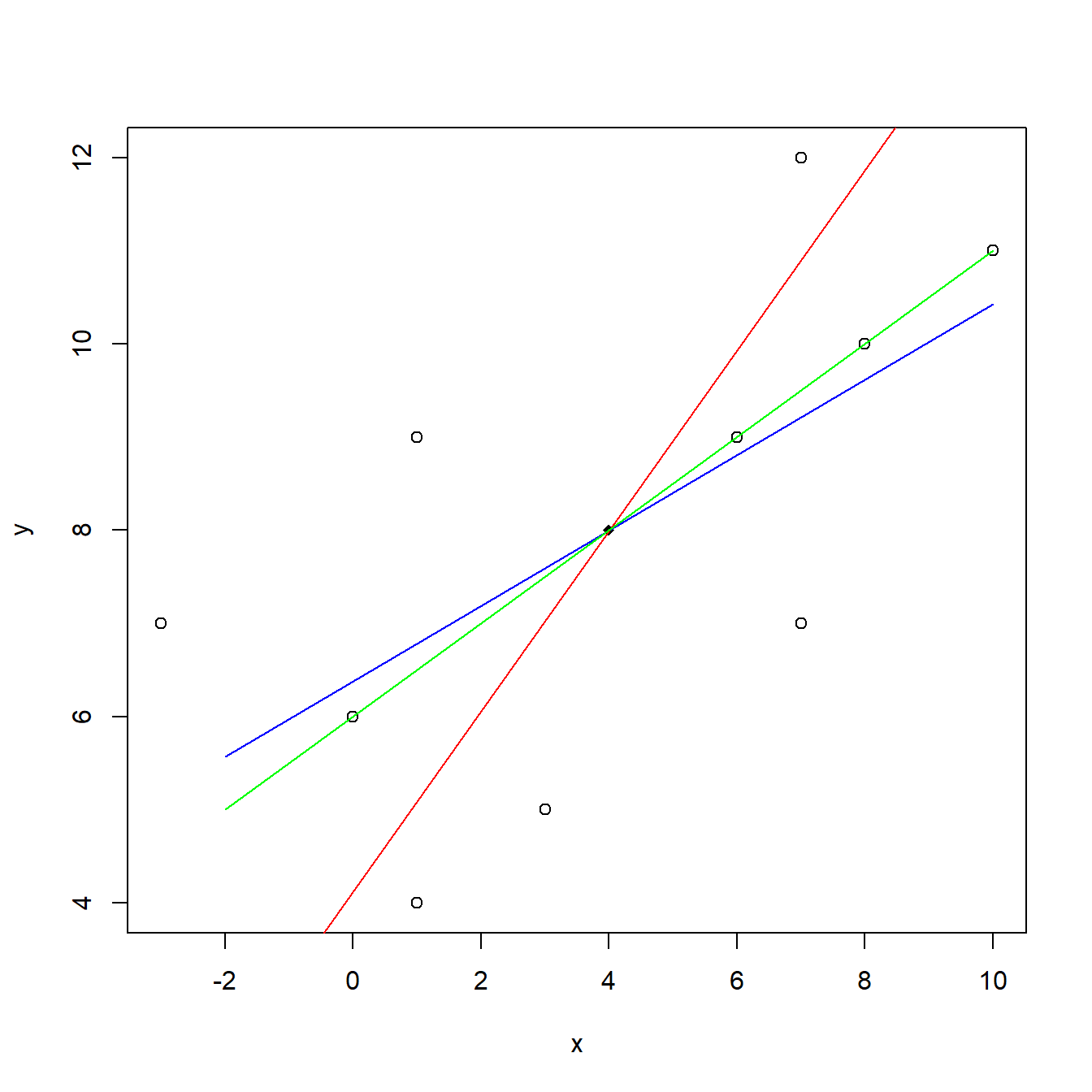
Figura 4.4: Diagrama de dispersión, junto con la primera componente principal (verde), la recta de regresión de \(y\) sobre \(x\) (azul) y la recta de regresión \(x\) de sobre \(y\) (rojo)