2.1 Estimación en la distribución normal multivariante

$ \newcommand{\bm}[1]{\boldsymbol{#1}} $ $ \newcommand{\textnormal}[1]{\textrm{#1}} $

2.1 Estimación en la distribución normal multivariante

2.1.1 La distribución normal multivariante

Recordamos que si una variable aleatoria $x$ unidimensional, con media $\mu$ y varianza $\sigma^2$ tiene distribución normal, entonces su función de densidad viene dada por

\[f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^\frac{-({x}-\mu)^2}{2\sigma^2},\ \ \ -\infty<x<\infty.\]

Decimos en este caso que $x$ tiene distribución $N(\mu,\sigma^2)$. Puedes ver la representación de la función de densidad de distintas variables normales en la Figura 2.1.

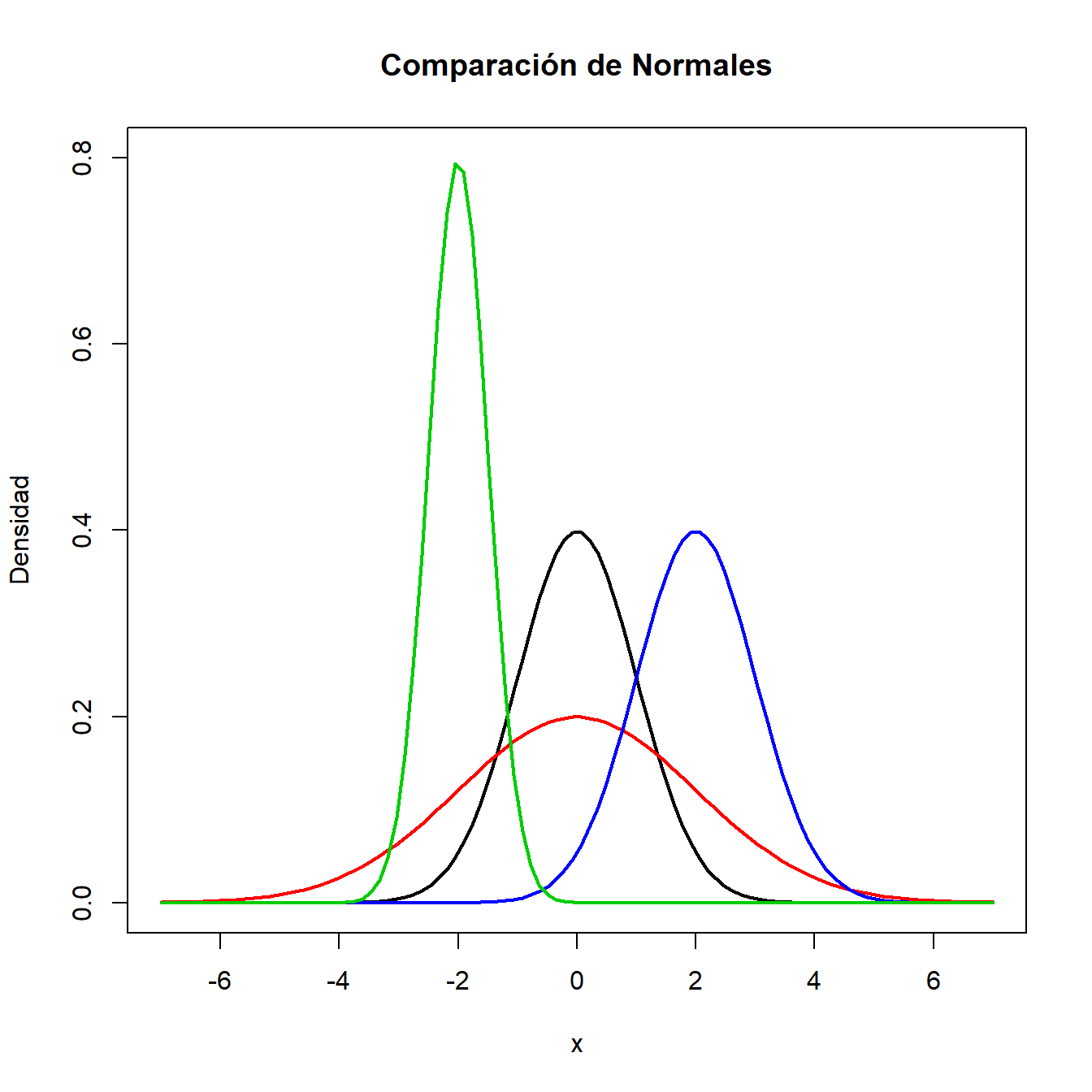
Figura 2.1: Representación de la densidad de variables normales.

Si el vector aleatorio $d$-dimensional $\bm{x}$ tiene distribución normal multivariante con vector de medias $\bm{\mu}$ y matriz de covarianzas $\bm\Sigma$, entonces su función de densidad viene dada por

\[f(\bm{x})=\frac{1}{(\sqrt{2\pi})^d\left|\bm\Sigma\right|^{1/2}}e^\frac{{-(\bm{x}-\bm{\mu})^\prime\bm{\Sigma}^{-1}(\bm{x}-\bm{\mu})}}{2}.\]

Decimos en este caso que $\bm{x}$ tiene distribución $N_d(\bm{\mu},\bm\Sigma)$. En la Figura 2.2 se representan las funciones de densidad de distintas variables normales bivariantes. En el Anexo A encontrarás propiedades importantes de esta distribución.

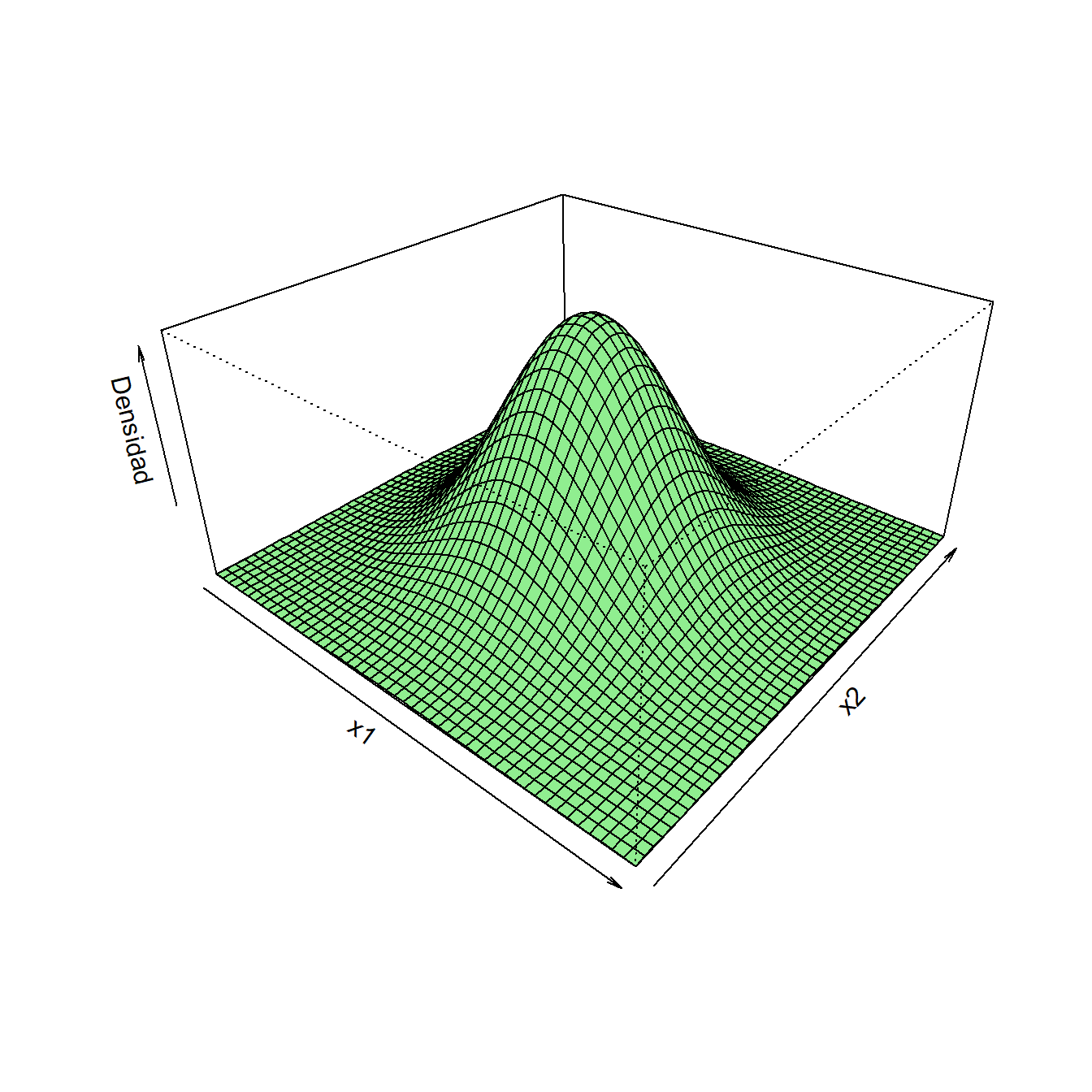
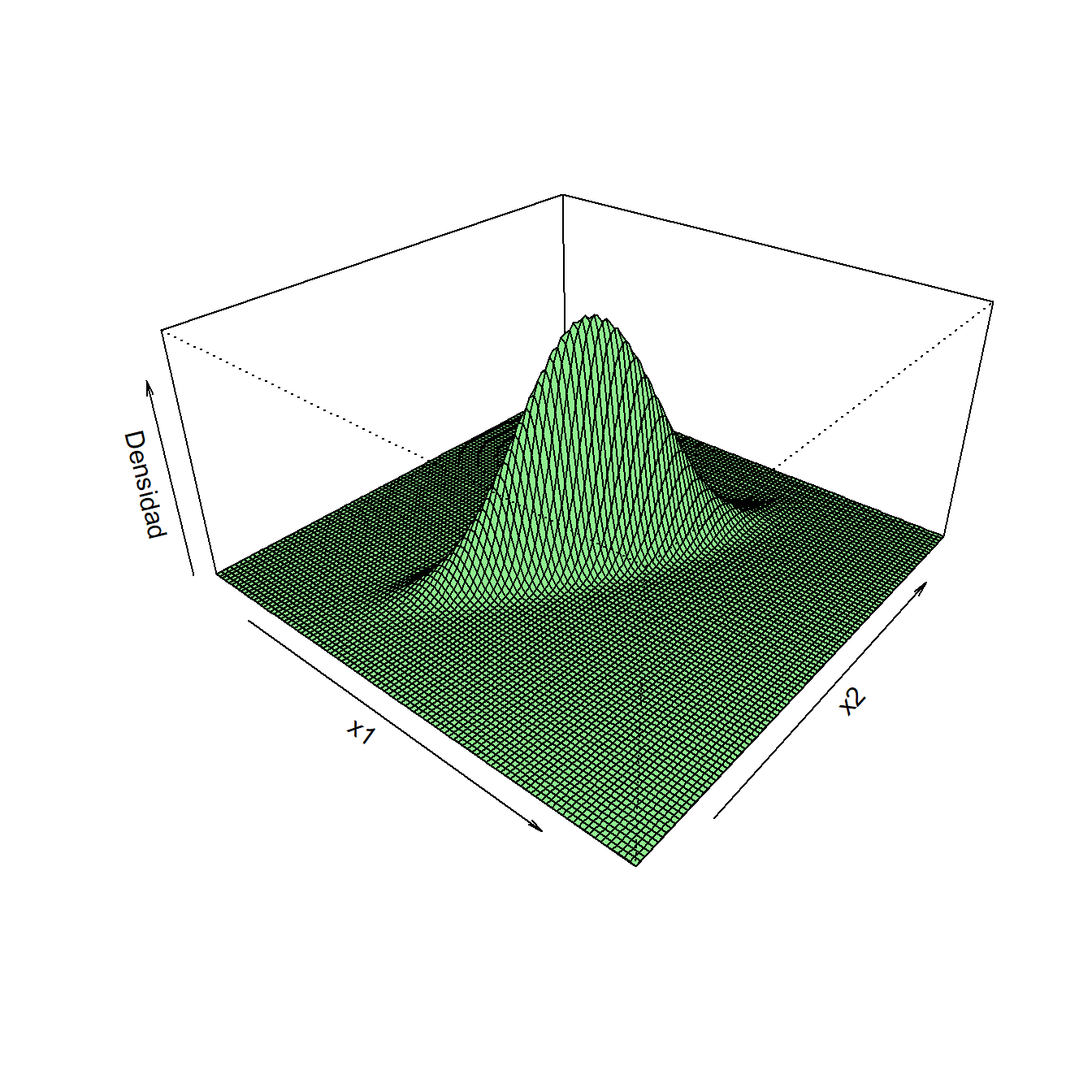
$Densidad de vectores aleatorios con distribución normal bivariante. A la izquierda $N(\bm{0},\bm{I_2})$. A la derecha $N(\bm{0},\bm{\Sigma})$ con $\sigma_1^2=1$, $\sigma_2^2=3$ y $\sigma_{12}=1.5$.$ $Densidad de vectores aleatorios con distribución normal bivariante. A la izquierda $N(\bm{0},\bm{I_2})$. A la derecha $N(\bm{0},\bm{\Sigma})$ con $\sigma_1^2=1$, $\sigma_2^2=3$ y $\sigma_{12}=1.5$.$

Figura 2.2: Densidad de vectores aleatorios con distribución normal bivariante. A la izquierda $N(\bm{0},\bm{I_2})$. A la derecha $N(\bm{0},\bm{\Sigma})$ con $\sigma_1^2=1$, $\sigma_2^2=3$ y $\sigma_{12}=1.5$.

Fíjate que en la densidad multivariante, $\left|\bm\Sigma\right|^{1/2}$ juega el papel de $\sqrt{\sigma^2}$ en el caso unidimensional. Decimos que $\left|\bm\Sigma\right|$ es la varianza poblacional generalizada. En efecto, el determinante $\left|\bm\Sigma\right|$ nos sirve como una medida de variabilidad total. Dado un vector aleatorio $\bm{x}$ con media $\bm{\mu}$ y matriz de covarianzas $\bm{\Sigma}$, un valor pequeño de $\left|\bm\Sigma\right|$ indica que $\bm{x}$ está concentrado cerca de $\bm{\mu}$ o que existe multicolinealidad entre las variables. Si recordamos que el determinante de una matriz es el producto de sus autovalores, podemos concebir el determinante como una medida de si una matriz de covarianzas es grande o pequeña. Por ejemplo, si existe multicolinealidad, uno o más autovalores de $\bm\Sigma$ será próximo a cero y en consecuencia, $\left|\bm\Sigma\right|$ será pequeño.

Podemos representar una matriz de covarianzas $2\times 2$ mediante una elipse cuyos ejes principales siguen la dirección de sus autovectores. Cada radio de la elipse es la raíz cuadrada de un autovalor de la matriz de covarianzas, ver Figura 2.3 (izquierda). Entonces, si denotamos por $\lambda_1$ y $\lambda_2$ a los autovalores de $\bm\Sigma$,

\[\textnormal{Area del rectángulo circunscrito en la elipse}=4\cdot \sqrt{\lambda_1}\sqrt{\lambda_2}=4\sqrt{\left|\bm\Sigma\right|}.\] En la última igualdad hemos usado que el determinante es el producto de los autovalores. En la Figura 2.3 (derecha) se representan las elipses correspondientes a distintas matrices de covarianzas. Para esta representación hemos utilizado la función ellipse de la librería car. En general, si la dimensión el espacio es $d$, se tendrá que

\[\textnormal{Volumen del rectángulo circunscrito en el elipsoide}=2^d\sqrt{\left|\bm\Sigma\right|}.\]

Empleamos los términos volumen y elipsoide, pues son los que corresponden en el espacio de dimensión tres. En espacios de dimensión superior, que no son representables, se suele emplear igualmente esos términos. Por tanto, el determinante es una forma de medir el volumen o capacidad de un rectángulo ($d=2$), caja ($d=3$), ortoedro en general, que contenga al grueso del vector.

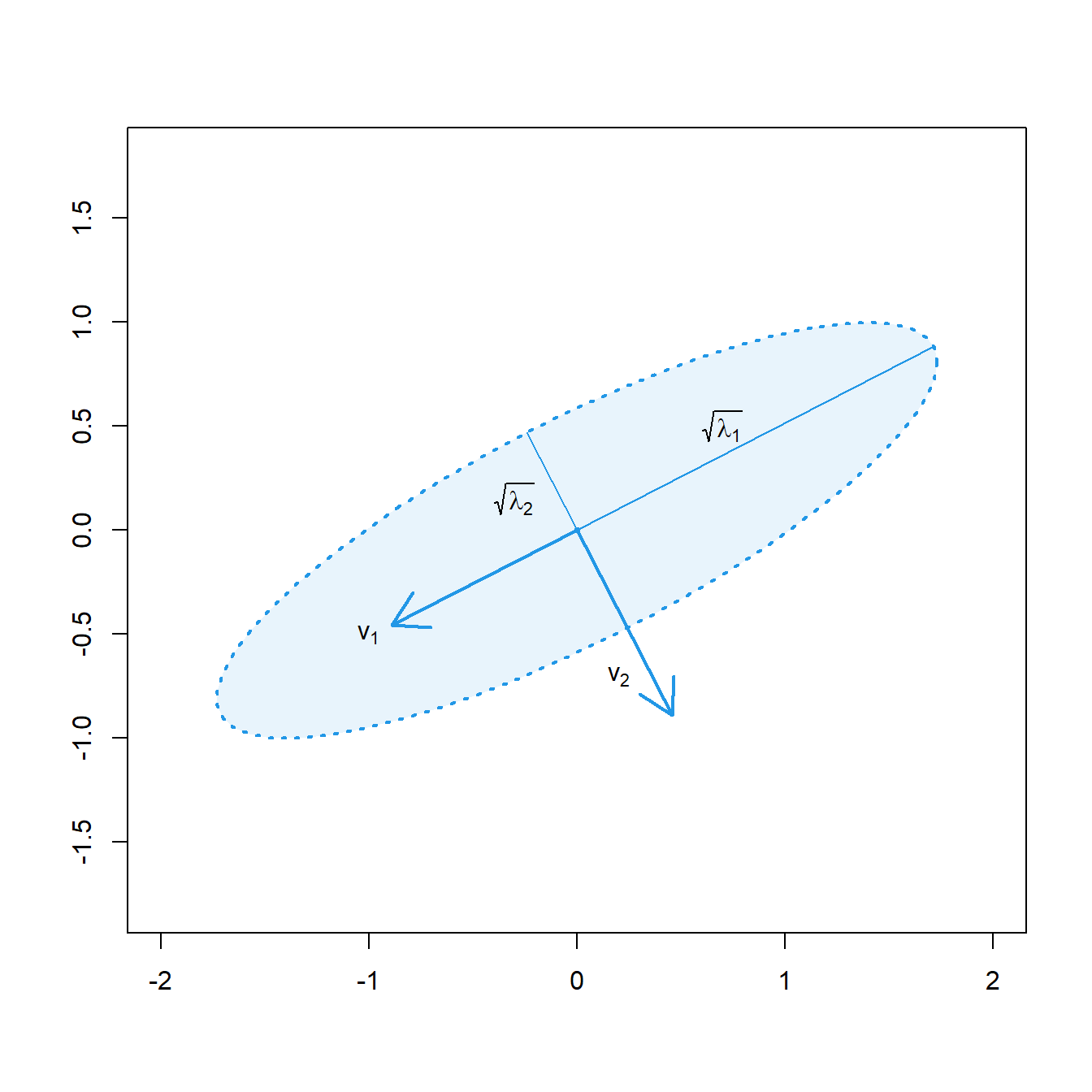
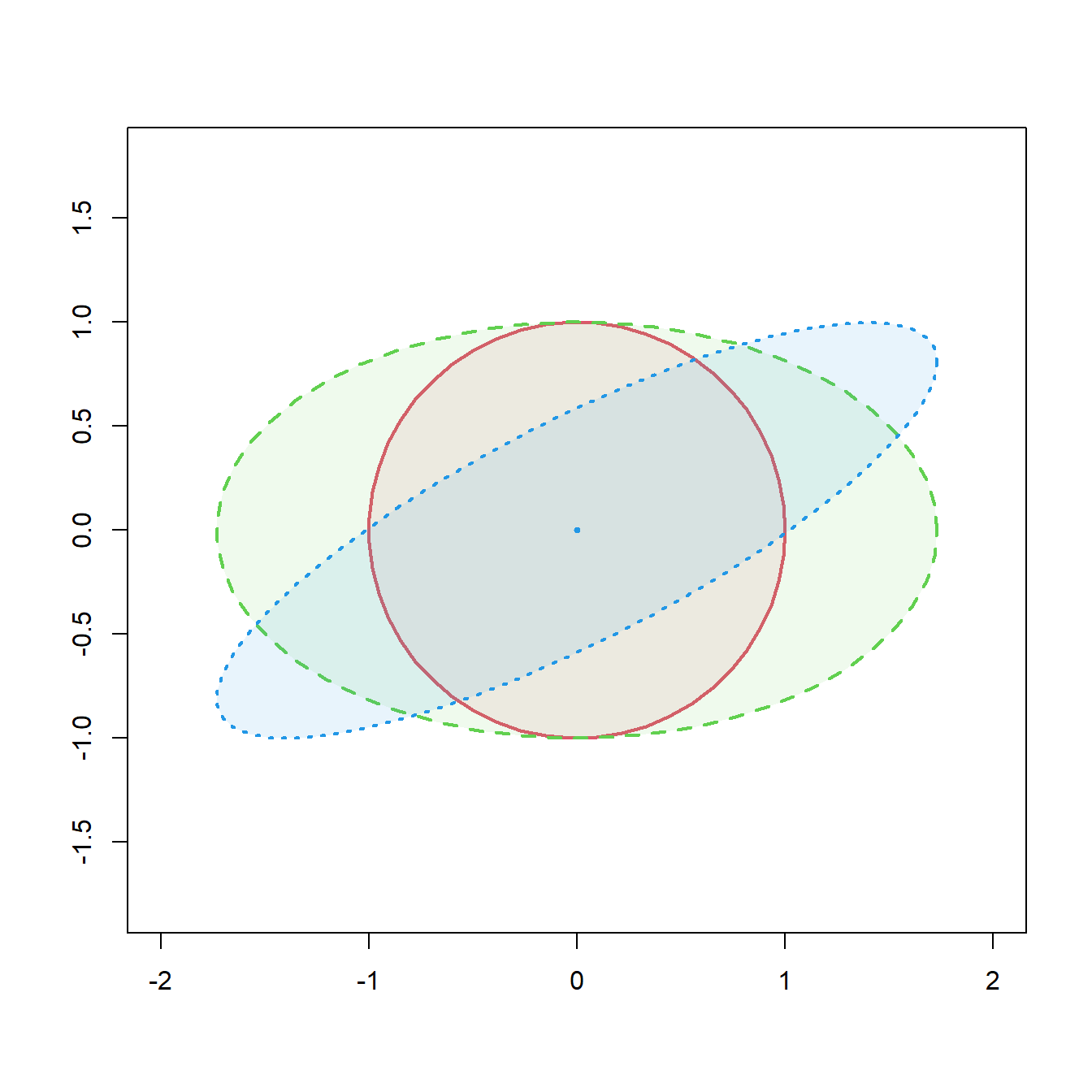
$Izquierda, representación de la elipse correspondiente a una matriz de covarianzas $2\times 2$. con autovectores $\bm{v_1}$, $\bm{v_2}$ y autovalores $\lambda_1$, $\lambda_2$. Cada radio de la elipse es la raíz cuadrada de un autovalor de la matriz de covarianzas. Derecha, representación de las elipses correspondientes a matrices de covarianzas $\bm{\Sigma_1}=\bm{I_2}$ (rojo), $\bm{\Sigma_2}=\mbox{diag}(3,1)$ (verde) y $\bm{\Sigma_3}=(\sigma_{ij})$ con $\sigma_{11}=3$, $\sigma_{22}=1$, $\sigma_{12}=1.4$ (azul).$ $Izquierda, representación de la elipse correspondiente a una matriz de covarianzas $2\times 2$. con autovectores $\bm{v_1}$, $\bm{v_2}$ y autovalores $\lambda_1$, $\lambda_2$. Cada radio de la elipse es la raíz cuadrada de un autovalor de la matriz de covarianzas. Derecha, representación de las elipses correspondientes a matrices de covarianzas $\bm{\Sigma_1}=\bm{I_2}$ (rojo), $\bm{\Sigma_2}=\mbox{diag}(3,1)$ (verde) y $\bm{\Sigma_3}=(\sigma_{ij})$ con $\sigma_{11}=3$, $\sigma_{22}=1$, $\sigma_{12}=1.4$ (azul).$

Figura 2.3: Izquierda, representación de la elipse correspondiente a una matriz de covarianzas $2\times 2$. con autovectores $\bm{v_1}$, $\bm{v_2}$ y autovalores $\lambda_1$, $\lambda_2$. Cada radio de la elipse es la raíz cuadrada de un autovalor de la matriz de covarianzas. Derecha, representación de las elipses correspondientes a matrices de covarianzas $\bm{\Sigma_1}=\bm{I_2}$ (rojo), $\bm{\Sigma_2}=\mbox{diag}(3,1)$ (verde) y $\bm{\Sigma_3}=(\sigma_{ij})$ con $\sigma_{11}=3$, $\sigma_{22}=1$, $\sigma_{12}=1.4$ (azul).

2.1.2 Estimadores de máxima verosimilitud

Consideremos disponible una muestra aleatoria simple $\bm{x_1},\ldots,\bm{x_n}\in N_d(\bm\mu,\bm\Sigma)$ de vectores aleatorios independientes y con la misma distribución normal multivariante. Vamos a obtener los estimadores de máxima verosimilitud para el vector de medias $\bm\mu$ y para la matriz de covarianzas $\bm\Sigma$. La función de verosimilitud sería:

\[L(\bm{x},\bm\mu,\bm\Sigma)=(2\pi)^{-nd/2} |\bm\Sigma |^{-n/2} \exp\left\{-\frac{1}{2}\sum_{i=1}^n \left(\bm{x_i}-\bm\mu\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\bm\mu\right)\right\}.\]

Observamos que

\[\begin{aligned} \sum_{i=1}^n \left(\bm{x_i}-\bm{\mu}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\bm{\mu}\right) &= \sum_{i=1}^n\left[ \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right)\right.\\ &\left.\qquad + \left(\overline{\bm{x}}-\bm{\mu}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu}\right)+ 2 \left(\overline{\bm{x}}-\bm{\mu}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right) \right] \\ &= \sum_{i=1}^n \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right)+ n \left(\overline{\bm{x}}-\bm{\mu}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu}\right) \end{aligned},\] ya que la suma de los dobles productos vale cero. Entonces la log–verosimilitud se puede expresar así:

\[\begin{aligned} \log L(\bm{x},\bm{\mu},\bm\Sigma) &= c - \frac{n}{2} \log |\bm\Sigma| - \frac{1}{2}\sum_{i=1}^n \left(\bm{x_i}-\bm{\mu}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\bm{\mu}\right) \\ &= c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \sum_{i=1}^n \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right)\\ &\qquad -\frac{n}{2} \left(\overline{\bm{x}}-\bm{\mu}\right)^\prime{}\bm\Sigma^{-1} \left(\overline{\bm{x}}-\bm{\mu}\right)\end{aligned}\] siendo $c=-\frac{nd}{2}\log(2\pi)$.

Observamos que, por ser $\bm\Sigma$ definida positiva, (y en consecuencia, también lo será su inversa $\bm\Sigma^{-1}$), se tiene $(\overline{\bm{x}}-\bm{\mu})^\prime{}\bm\Sigma^{-1}(\overline{\bm{x}}-\bm{\mu})>0$, salvo que $\bm{\mu}=\overline{\bm{x}}$, en cuyo caso vale cero. Por tanto, la función de log–verosimilitud alcanza su máximo en $\hat{\bm{\mu}}=\overline{\bm{x}}$, que de este modo se convierte en el estimador de máxima verosimilitud del vector de medias. Además,

\[\begin{equation} \sup_{\bm\mu}\log L(\bm{x},\bm\mu,\bm\Sigma) = c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \sum_{i=1}^n \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right) \tag{2.1} \end{equation}\]

para cualquier matriz de covarianzas $\bm\Sigma$.

A continuación calcularemos el máximo de aquella función respecto de $\bm\Sigma$. Podemos expresar

\[\begin{aligned} \sup_{\bm{\mu}}\log L(\bm{x},\bm{\mu},\bm\Sigma) &= c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \mbox{traza} \left[\sum_{i=1}^n \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{}\bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right)\right] \nonumber \\ &= c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \sum_{i=1}^n \mbox{traza} \left[\left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{} \bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right)\right] \nonumber \\ &= c - \frac{n}{2} \log |\bm\Sigma| -\frac{1}{2} \sum_{i=1}^n \mbox{traza} \left[ \bm\Sigma^{-1} \left(\bm{x_i}-\overline{\bm{x}}\right) \left(\bm{x_i}-\overline{\bm{x}}\right)^\prime{} \right] \nonumber \\ &= c - \frac{n}{2}\left( \log |\bm\Sigma| + \mbox{traza} \left( \bm\Sigma^{-1} \bm{S} \right)\right) \end{aligned}\] donde hemos aplicado que traza($\bm{A}$+$\bm{B}$)=traza($\bm{A}$)+traza($\bm{B}$) y que traza($\bm{AB}$)=traza($\bm{BA}$). Ahora debemos obtener el máximo de esta función respecto del argumento $\bm\Sigma$. Para ello, apelamos al resultado siguiente, del cual omitimos su demostración.

Lema 2.1 Supongamos una matriz $\bm{A}$ definida positiva. La función

\[f(\bm\Sigma)=\log|\bm\Sigma|+{\textnormal{traza}}\left(\bm\Sigma^{-1}\bm{A}\right),\] restringida a las matrices $\bm\Sigma$ definidas positivas, alcanza su mínimo en $\bm\Sigma=\bm{A}$.

Entonces, aplicando este lema llegamos a la conclusión de que los estimadores de máxima verosimilitud del vector de medias y la matriz de covarianzas (sin restricciones) son $\overline{\bm{x}}$ y $\bm{S}$, respectivamente. Asimismo, la función de verosimilitud tiene como máximo:

\[\begin{aligned} \sup_{\bm\Sigma}\sup_{\bm\mu}\log L(\bm{x},\bm{\mu},\bm\Sigma) &= c - \frac{n}{2} \left( \log |\bm{S}| + \mbox{traza} \left( \bm{S}^{-1} \bm{S} \right)\right)\\ &= c - \frac{n}{2} \left( \log |\bm{S}| + d\right). \end{aligned}\]

2.1.3 Distribución de $\overline{\bm{x}}$ y $\bm{S}$

Sea entonces $\bm{x_1},\ldots,\bm{x_n}$ una muestra aleatoria simple de $N_d(\bm\mu,\bm\Sigma)$. En el apartado anterior hemos visto que los estimadores de máxima verosimilitud de $\bm\mu$ y $\bm\Sigma$ son $\overline{\bm{x}}$ y $\bm{S}$, respectivamente. Se verifica que:

\[\overline{\bm{x}}=\frac{1}{n}\sum_{i=1}^n \bm{x_i} \in N_d\left(\bm{\mu},\frac{1}{n}\bm\Sigma\right).\]

Se puede ver este resultado como una generalización del caso unidimensional. Recuerda que si ${x_1},\ldots,{x_n}$ es una muestra aleatoria simple de $N(\mu,\sigma^2)$, entonces $\overline{{x}}\in N\left({\mu},\sigma^2/n\right)$. Además en el caso unidimensional se demostraba también que $ns^2/\sigma^2=\sum_{i=1}^n(x_i-\bar{x})^2/\sigma^2\in \chi_{n-1}^2$, es decir, tiene distribución ji-cuadrado con $n-1$ grados de libertad². Una forma de generalizar la suma de cuadrados anterior al caso multivariante sería considerar

\[n\bm{S}=\sum_{i=1}^n(\bm{x_i}-\overline{\bm{x}})(\bm{x_i}-\overline{\bm{x}})^\prime{}.\]

Fíjate que $n\bm{S}$ es una matriz aleatoria $d\times d$ y por tanto su distribución ya no podrá ser ji-cuadrado como en el caso unidimensional. Decimos que $n\bm{S}$ sigue una distribución de Wishart³ con parámetros $\bm\Sigma$ y $n-1$ y denotamos:

\[n\bm{S}=\sum_{i=1}^n(\bm{x_i}-\bm{\bar{x}})(\bm{x_i}-\bm{\bar{x}})^\prime{}\in W_d(\bm\Sigma,n-1).\] En el Anexo A puedes encontrar un resumen de las principales propiedades de la distribución de Wishart.

La distribución ji-cuadrado se define formalmente como la suma de los cuadrados de variables normales estándar, es decir si ${x_1},\ldots,{x_n}$ son $N(\mu,\sigma^2)$ independientes, entonces $\sum_{i=1}^n(x_i-\mu)^2/\sigma^2\in \chi_{n}^2$.↩︎
La distribución de Wishart es el análogo multivariante de la distribución ji-cuadrado y se define formalmente a partir de normales multivariantes estándar. Si $\bm{x_1},\ldots,\bm{x_n}$ son $N_d(\bm\mu,\bm\Sigma)$ independientes, entonces \[\sum_{i=1}^n(\bm{x_i}-\bm{\mu})(\bm{x_i}-\bm{\mu})^\prime{}\in W_d(\bm\Sigma,n).\] Cuando sustituimos $\bm\mu$ por $\overline{\bm{x}}$, la distribución de Wishart pierde un grado de libertad.↩︎