5.4 Representación simultánea de los perfiles de fila y columna
Consideremos la matriz
\[\bm{Z}=\left( \frac{f_{ij}}{\sqrt{f_{i\bullet}}\sqrt{f_{\bullet j}}} \right)_{i,j}.\]
Observemos que
\[\bm{X}=\bm{D_r}^{-1}\bm{F} \bm{D_s}^{-1/2},\ \ \ \ \bm{Y}=\bm{D_r}^{-1/2} \bm{F} \bm{D_s}^{-1},\ \ \ \ \bm{Z}=\bm{D_r}^{-1/2} \bm{F}\bm{D_s}^{-1/2}\] siendo \(\bm{F}=\left(f_{ij}\right)_{i,j}\). Entonces
\(\bm{X}^{\prime} \bm{D_r} \bm{X}=\bm{Z}^{\prime} \bm{Z}\qquad \bm{Y \bm{D_s} \bm{Y}^{\prime}}=\bm{Z}\bm{Z}^{\prime}.\)
Si \(\bm{v}\) es autovector de \(\bm{Z}^{\prime} \bm{Z}\) con autovalor asociado \(\lambda\), entonces \(\bm{w}=\bm{Z}\bm{v}\) es autovector de \(\bm{Z}\bm{Z}^{\prime}\) con autovalor asociado \(\lambda\).
Por tanto, ambas matrices tienen los mismos autovalores, mientras que los autovectores mantienen la relación que se acaba de indicar. Como consecuencia, el número de autovalores no nulos será \(k_0\leq \min\{r,s\}\). En lo que sigue supondremos una matriz común de autovalores no nulos \(\bm{D_{\lambda}}\) de orden \(k_0\), y los autovectores y coordenadas se referirán únicamente a las \(k_0\) componentes asociadas a estos autovalores no nulos, tanto cuando se interpreten en el espacio de filas como en el de columnas.
Recordemos la diagonalización
\[\bm{Z}^{\prime} \bm{Z}= \bm{X}^{\prime} \bm{D_r} \bm{X}= \bm{V}\bm{D_{\lambda}}\bm{V}^{\prime}.\] Entonces las columnas de \(\bm{ZV}\) son los autovectores de \(\bm{Z}\bm{Z}^{\prime}\), que una vez normalizadas darán lugar a la matriz ortogonal para la diagonalización \(\bm{Z}\bm{Z}^{\prime}= \bm{W}\bm{D_{\lambda}} \bm{W}^{\prime}\):
\[\bm{W}=\bm{Z}\bm{VD_{\lambda}}^{-1/2}.\] Finalmente, las coordenadas de los perfiles de columna eran las columnas de la matriz
\[\bm{B}=\bm{W}^{\prime}\bm{Y}.\] Vamos a deducir la relación que existe entre estas coordenadas y las coordenadas de los perfiles de fila, \(\bm{A}=\bm{XV}\).
\[\begin{aligned} \bm{B}&= \bm{W}^{\prime}\bm{Y}= \left(\bm{Z}\bm{V}\bm{D_{\lambda}}^{-1/2}\right)^{\prime} \bm{Y} =\bm{D_{\lambda}}^{-1/2}\bm{V}^{\prime} \bm{Z}^{\prime} \bm{Y} \\ &=\bm{D_{\lambda}}^{-1/2} \bm{V}^{\prime} \left(\bm{D_r}^{-1/2}\bm{F}\bm{D_s}^{-1/2}\right)^{\prime} \bm{D_r}^{-1/2}\bm{F}\bm{D_s}^{-1} =\bm{D_{\lambda}}^{-1/2} \bm{V}^{\prime} \bm{D_s}^{-1/2} \bm{F}^{\prime} \bm{D_r}^{-1} \bm{F}\bm{D_s}^{-1} \\ &=\bm{D_{\lambda}}^{-1/2} \bm{A}^{\prime} \bm{F}\bm{D_s}^{-1}. \end{aligned}\] En la última igualdad se ha utilizado que \(\bm{A}=\bm{X}\bm{V}=\bm{D_r}^{-1}\bm{F}\bm{D_s}^{-1/2}\bm{V}\). Pero el resultado obtenido se puede escribir así:
\[b_{kj}=\frac{1}{\sqrt{\lambda_k}} \left( \frac{f_{1j}}{f_{\bullet j}} a_{1k} +\ldots + \frac{f_{rj}}{f_{\bullet j}} a_{rk} \right)\] de modo que la coordenada del perfil de columna \(j\)-ésimo en la componente \(k\)-ésima es una combinación ponderada de las coordenadas de cada perfil de fila en dicha componente, siendo los pesos de tal ponderación las frecuencias relativas de cada categoría de la variable \(x\) condicionada a la categoría j de \(y\). Así, si una categoría i presenta alta frecuencia condicionada pesará más en esta combinación, aproximando hacia sí la coordenada de la categoría \(j\) de la variable \(y\). De igual modo, se puede ver que
\[\bm{A}=\bm{D_r}^{-1}\bm{F}\bm{B}^{\prime}\bm{D_{\lambda}}^{-1/2}.\]
Ejemplo. En el ejemplo sobre los datos de la EPA (2010), vamos a representar en un mismo gráfico bidimensional los perfiles de fila y columna.
> library(MASS) # Cargamos el paquete MASS (Venables y Ripley)
> m <- cbind(dat$Ocupados, dat$Parados, dat$Inactivos) # Frecuencias absolutas
> rownames(m) <- dat$Comunidad.Autónoma # Nombres de filas
> colnames(m) <- names(dat)[2:4] # Nombres de las columnas
> r <- nrow(m) # Número de filas
> s <- ncol(m) # Número de columnas
> n <- sum(m) # Frecuencia total (tamaño muestral)
> f <- m/n # Frecuencias relativas (conjuntas)
> mx <- apply(f, 1, sum) # Frecuencias marginales de columna
> my <- apply(f, 2, sum) # Frecuencias marginales de filaCalculamos los perfiles de fila y columna.
> ri <- diag(1/mx) %*% f # Perfiles de fila
> rownames(ri) <- dat$Comunidad.Autónoma
> cj <- f %*% diag(1/my) # Perfiles de columna
> colnames(cj) <- names(dat)[2:4]A continuación, calculamos las componentes principales de los perfiles de fila estandarizados.
> x <- ri %*% diag(1/sqrt(my)) # Perfiles de fila estandarizados
> mye <- sqrt(my) # Marginal de fila estandarizada
> sr <- t(x) %*% diag(mx) %*% x - mye %*% t(mye) # Matriz Sigma_r
> auto <- eigen(t(x) %*% diag(mx) %*% x) # Diagonalización
> lam <- auto$values # Autovalores
> v <- auto$vectors # AutovectoresCalculamos ahora las coordenadas de los perfiles de fila estandarizados en las componentes y hacemos la representación (Figura 5.1).
> a <- x %*% v
> plot(a[, 2], a[, 3])
> text(a[, 2], a[, 3], labels = dat$Comunidad.Autónoma)
> abline(h = 0, lty = 2)
> abline(v = 0, lty = 2)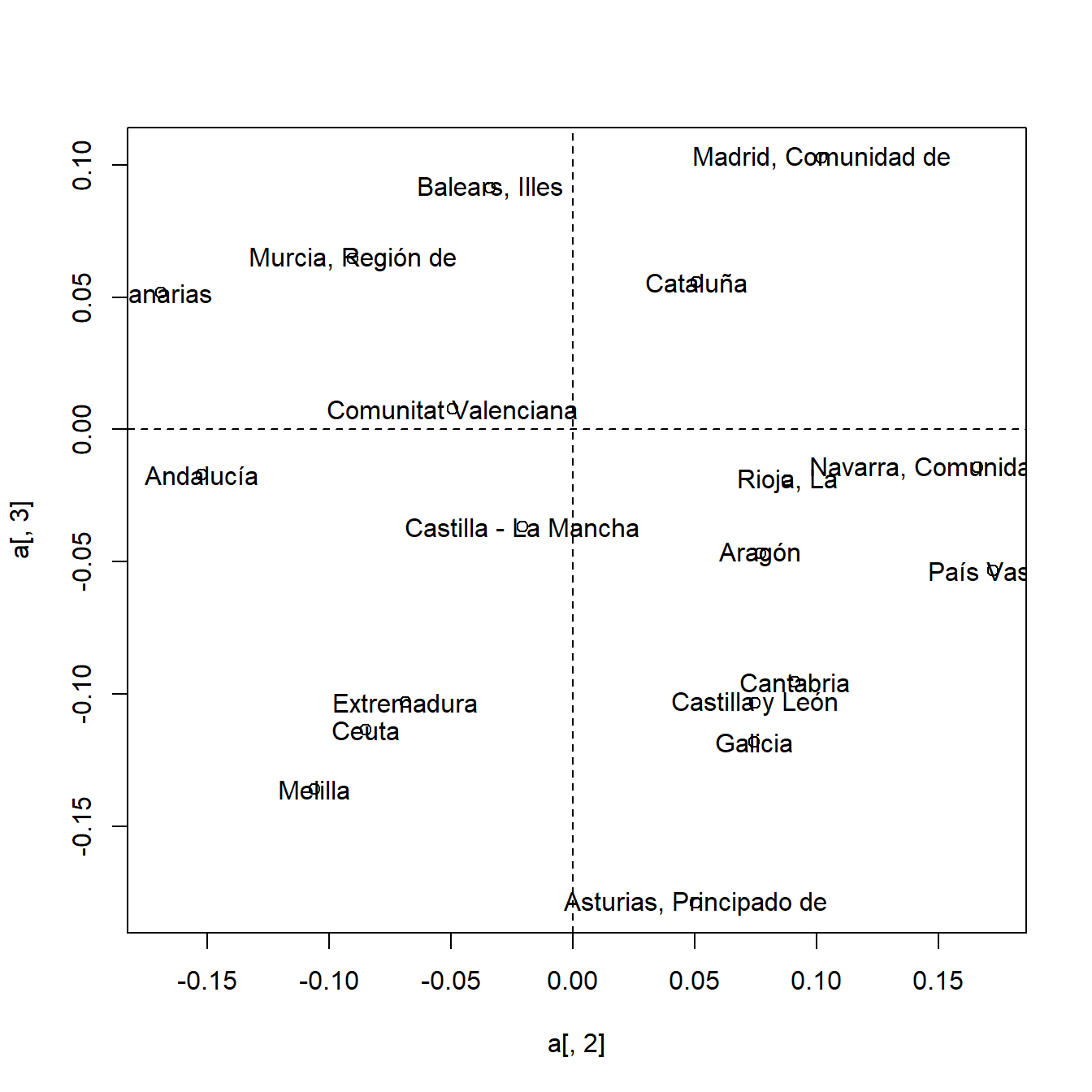
Figura 5.1: Gráficos de perfiles de fila.
A continuación, calculamos las componentes principales de los perfiles de columna estandarizados.
> y <- diag(1/sqrt(mx)) %*% cj # Perfiles de columna estandarizados
> mxe <- sqrt(mx) # Marginal de columna estandarizada
> sigs <- y %*% diag(my) %*% t(y) - mxe %*% t(mxe) # Matriz Sigma_s
> auto <- eigen(y %*% diag(my) %*% t(y)) # Diagonalización
> lam <- auto$values # Autovalores
> w <- auto$vectors # AutovectoresCalculamos ahora las coordenadas de los perfiles de columna estandarizados en las componentes y hacemos la representación (Figura 5.2).
> b <- t(w) %*% y
> plot(b[2, ], b[3, ])
> text(b[2, ], b[3, ], names(dat)[2:4])
> abline(h = 0, lty = 2)
> abline(v = 0, lty = 2)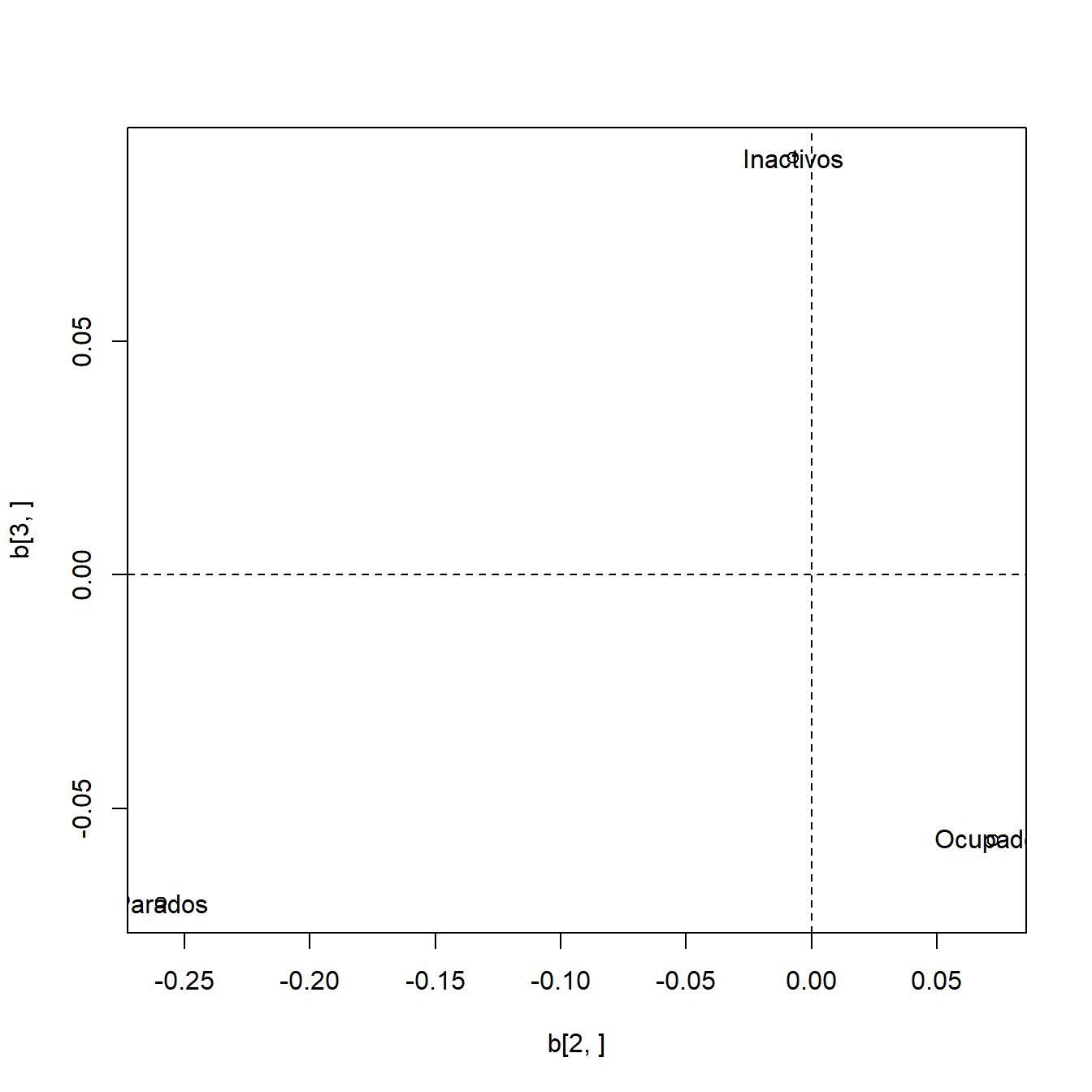
Figura 5.2: Gráficos de perfiles de columna.
Hacemos ahora la representación simultánea (Figura 5.3).
> z <- diag(1/sqrt(mx)) %*% f %*% diag(1/sqrt(my))
> k0 <- 3
> w <- z %*% v[, 1:k0] %*% diag(1/sqrt(lam[1:k0]))
> b <- t(w) %*% y
> plot(c(a[, 2], b[2, ]), c(a[, 3], b[3, ]))
> text(c(a[, 2], b[2, ]), c(a[, 3], b[3, ]),
+ labels = c(as.character(dat$Comunidad.Autónoma), names(dat)[2:4]),
+ col = c(rep("blue", r), rep("red", s)), cex = 0.7)
> abline(h = 0, lty = 2)
> abline(v = 0, lty = 2)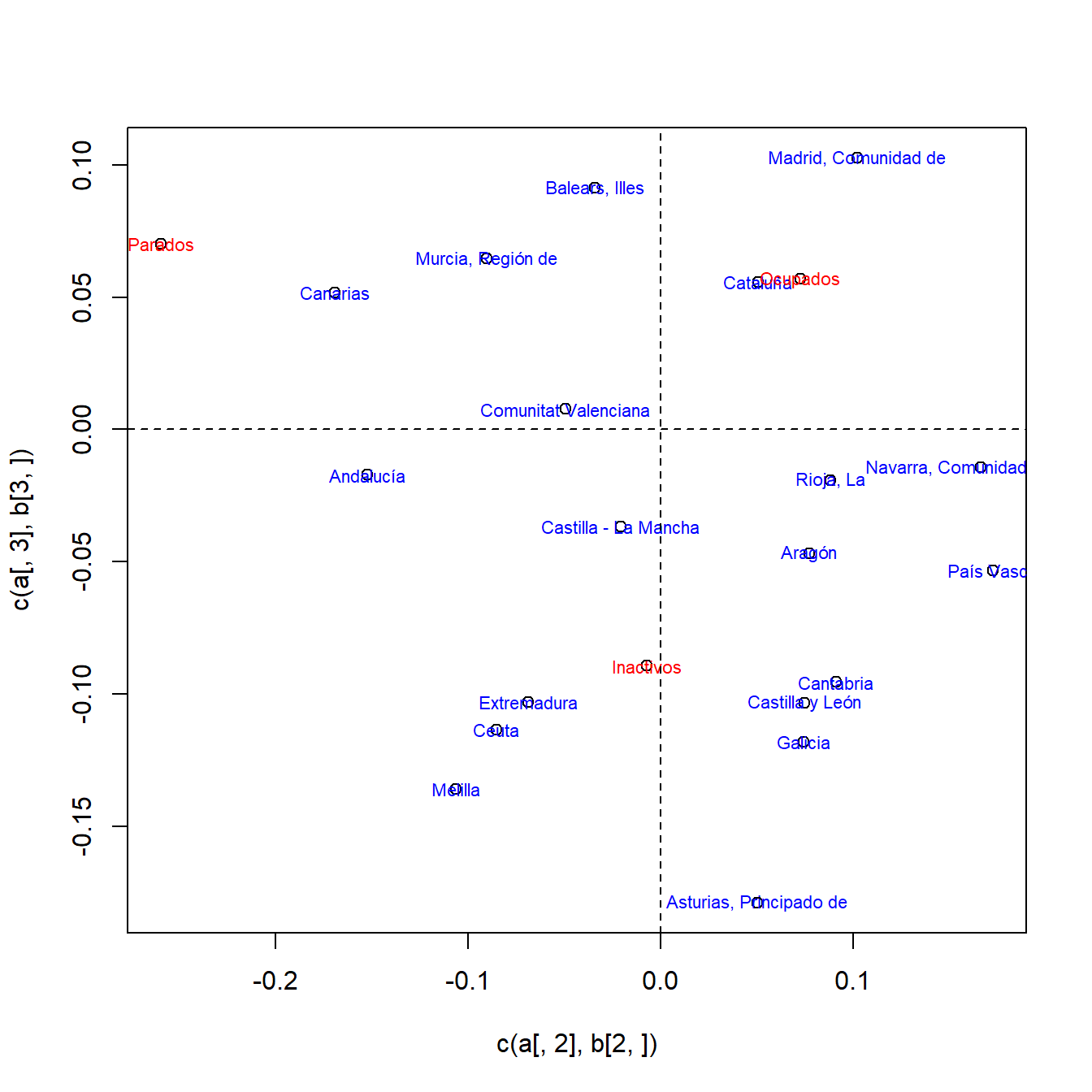
Figura 5.3: Representación simultánea de los perfiles de fila y columna para los datos de la EPA.
También podemos hacer la representación utilizando el comando corresp.
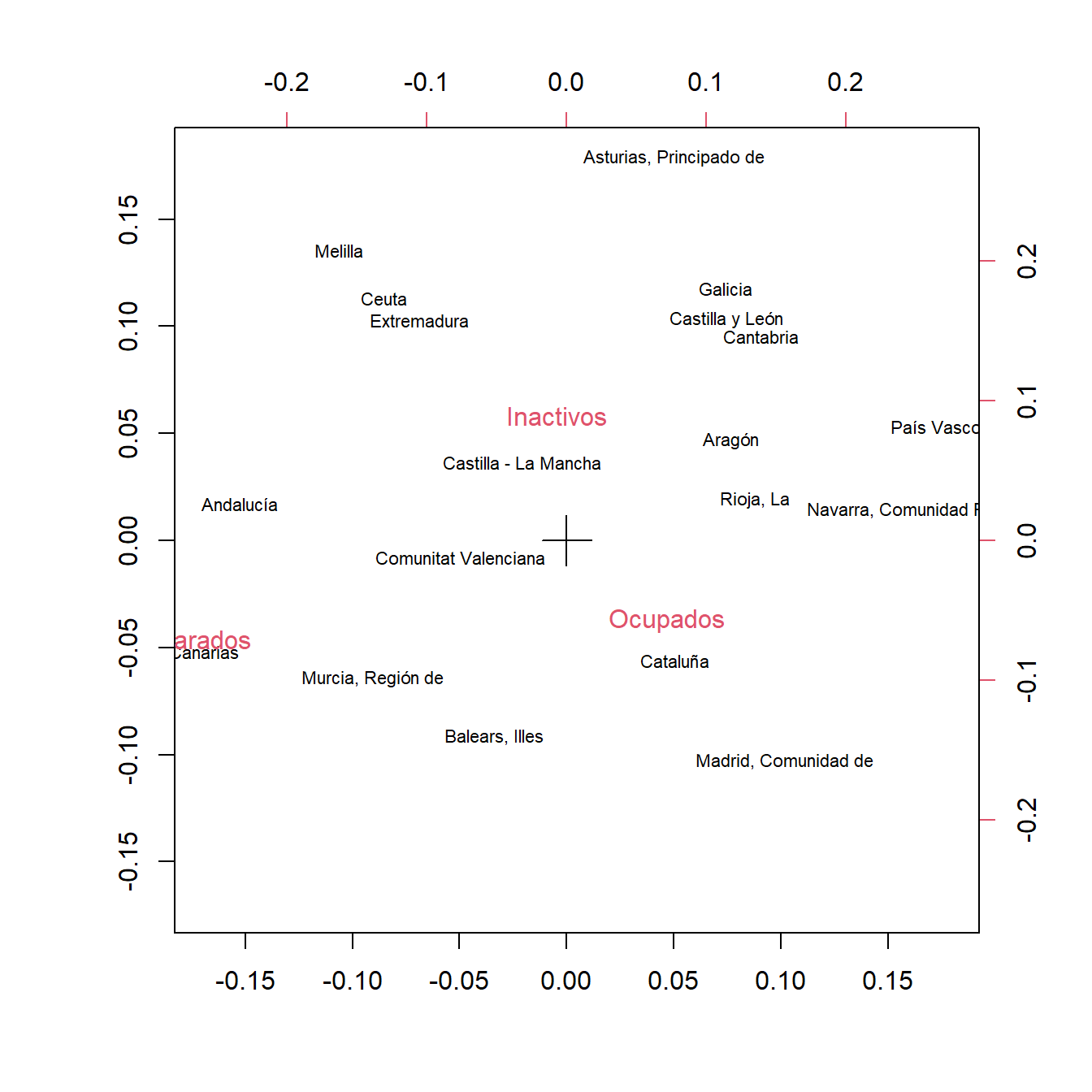
Figura 5.4: Representación simultánea de los perfiles de fila y columna para los datos de la EPA (función corresp).
El resultado se muestra en la Figura 5.4. El eje horizontal corresponde a la primera componente y el eje vertical a la segunda. La proximidad entre los puntos de distintas comunidades autónomas indica que presentan perfiles similares. Asimismo, si una comunidad autónoma está próxima al punto correspondiente a los Inactivos, esto indica que en su perfil hay un porcentaje alto de población inactiva. Igualmente para las categorías de Ocupados y Parados.