2.4 Regiones de confianza y comparaciones simultáneas
2.4.1 Regiones de confianza
A partir del estadístico \(\Gamma^2\) de Hotelling, podemos obtener una región de confianza para el vector de medias, de la forma:
\[\left\{\bm{\mu}\in{\Bbb R}^d: \frac{n-d}{d}\left(\overline{\bm{x}}-\bm{\mu}\right)^\prime{}\bm{S}^{-1}\left(\overline{\bm{x}}-\bm{\mu}\right)<f_{d,n-d,\alpha}\right\}.\]
Esta región constituye un elipsoide en \({\Bbb R}^d\), centrado en \(\overline{\bm{x}}\), cuyos ejes van en la dirección de los autovectores de \(\bm{S}\) y la longitud de los radios (semilongitud de los ejes) viene dada por
\[\sqrt{\lambda_j}\sqrt{\frac{d}{n-d}f_{d,n-d,\alpha}}\qquad j\in\{1,\ldots,d\}\]
siendo \(\lambda_1,\ldots,\lambda_d\) los autovalores de \(\bm{S}\). En la Figura 2.6 se muestra la región de confianza (\(\alpha=0.05\)) para el vector de notas medias en el ejemplo de tests de inteligencia. El elipsoide se calcula en base al estadístico \(\Gamma^2\) de Hotelling.
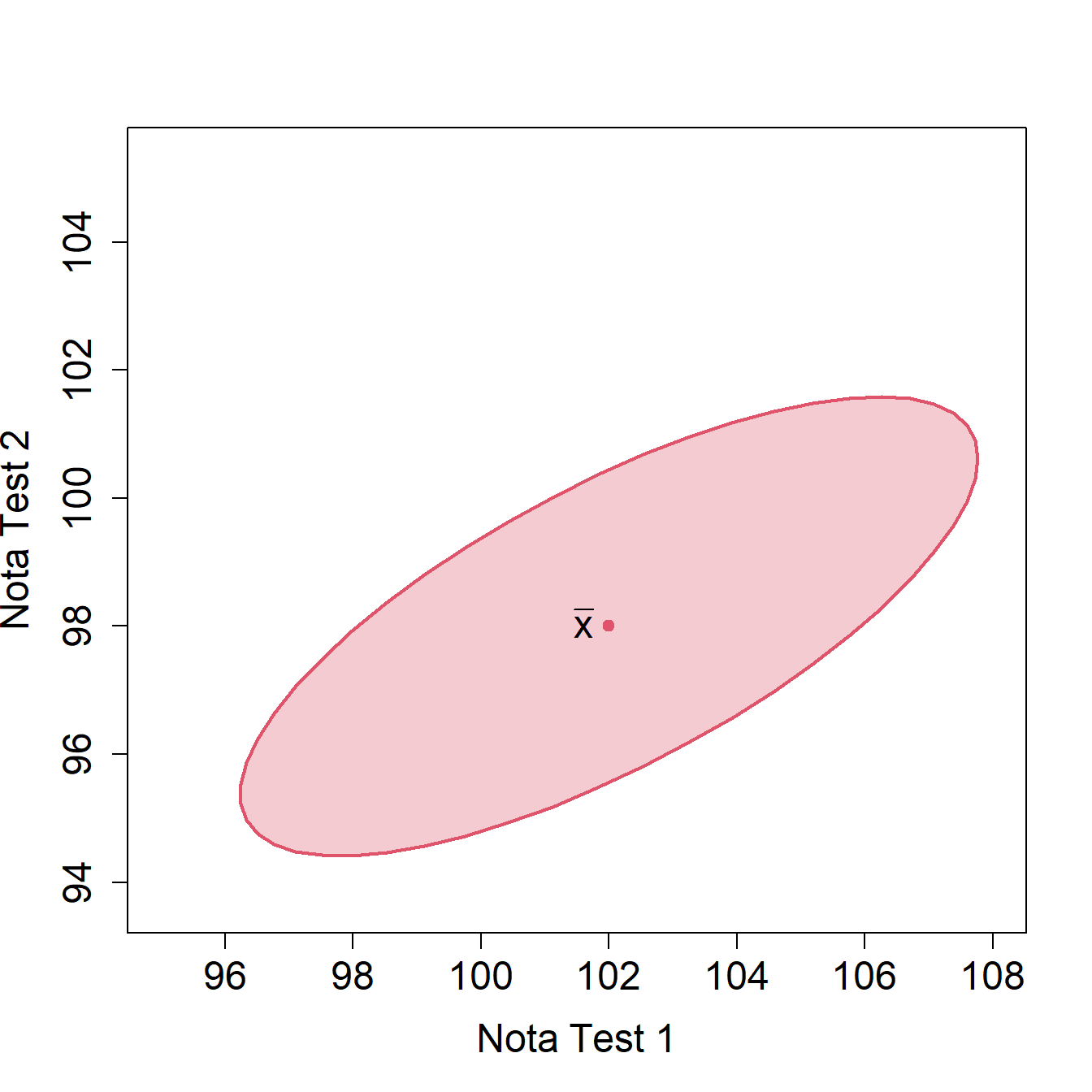
Figura 2.6: Región de confianza (\(\alpha=0.05\)) para el vector de notas medias en el ejemplo de tests de inteligencia.
2.4.2 Intervalos de confianza individuales
A continuación planteamos el problema de conseguir intervalos de confianza para las componentes del vector de medias, o más en general, para combinaciones lineales del tipo
\[\bm{a}^\prime{}\bm{\mu}=a_1\mu_1+\cdots+a_d\mu_d.\]
Observando que \(\bm{a}^\prime{}\bm{x_1},\ldots,\bm{a}^\prime{}\bm{x_n}\in N(\bm{a}^\prime{}\bm{\mu},\bm{a}^\prime{}\bm\Sigma\bm{a})\) y además son independientes, podemos abordar este problema, que ya es univariante, mediante el procedimiento de la \(t\) de Student. Así, como la media y la cuasivarianza muestrales calculadas sobre las observaciones \(\bm{a}^\prime{}\bm{x_1},\ldots,\bm{a}^\prime{}\bm{x_n}\) resultan ser \(\bm{a}^\prime{}\overline{\bm{x}}\) y \(\bm{a}^\prime{}\bm{S_c}\bm{a}\), respectivamente, el intervalo de confianza adopta la forma
\[\left(\bm{a}^\prime{}\overline{\bm{x}}-t_{n-1,\alpha/2}\frac{\sqrt{\bm{a}^\prime{}\bm{S_c}\bm{a}}}{\sqrt{n}}, \bm{a}^\prime{}\overline{\bm{x}}+t_{n-1,\alpha/2}\frac{\sqrt{\bm{a}^\prime{}\bm{S_c}\bm{a}}}{\sqrt{n}}\right)\] siendo \(t_{n-1,\alpha/2}\) el cuantil \(1-\alpha/2\) de la distribución \(t\) de Student con \(n-1\) grados de libertad. De este modo, para un \(\bm{a}\) fijo, el intervalo anterior contiene a \(\bm{a}^\prime{}\bm{\mu}\) con una probabilidad \(1-\alpha\). En particular, podemos pensar en un vector de la forma \(\bm{a}=(1,0,\ldots,0)^\prime{}\) que serviría para extraer la primera componente del vector aleatorio. Igual se haría con las demás componentes mediante los vectores canónicos correspondientes. Así obtendríamos \(p\) intervalos de confianza, uno para cada componente del vector de medias. Sin embargo, el nivel de confianza se refiere a la probabilidad individual de cada intervalo, de modo que la probabilidad de que todos los intervalos simultáneamente contengan a la componente correspondiente del vector de medias será en general inferior al nivel de confianza fijado.
2.4.3 Intervalos de confianza simultáneos por el método de Scheffé
Para satisfacer un nivel de confianza simultáneo, debemos modificar la construcción de los intervalos haciéndolos más amplios. Vamos a plantear este objetivo de manera simultánea en todos los vectores \(\bm{a}\). Si seguimos partiendo como pivote de la media estudentizada, la idea podría ser cambiar el valor \(t_{n-1,\alpha/2}\) por otra constante adecuada, previsiblemente más grande. Así, si
\[P\left\{ \left|\frac{\sqrt{n}\left(\bm{a}^\prime{}\overline{\bm{x}}-\bm{a}^\prime{}\bm{\mu}\right)}{\sqrt{\bm{a}^\prime{}\bm{S_c}\bm{a}}}\right| < c \qquad \forall \bm{a}\in{\Bbb R}^p\right\}=1-\alpha\] los intervalos de confianza obtenidos al sustituir \(t_{n-1,\alpha/2}\) por \(c\) cumplirán el nivel de confianza de manera simultánea. Enunciamos el lema siguiente.
Lema 2.2 Sea \(\bm{B}\) una matriz \(d\times d\), simétrica y definida positiva, y \(\bm{r}\in {\Bbb R}^d\). Entonces
\[\max_{\bm{x}\in{\Bbb{R}}^d\backslash\{\bm{0}\}}\frac{\left(\bm{x}^\prime{}\bm{r}\right)^2}{\bm{x}^\prime{}\bm{B}\bm{x}}=\bm{r}^\prime{}\bm{B}^{-1}\bm{r}\] y este máximo se alcanza cuando \(\bm{x}=c\bm{B}^{-1}\bm{r}\) para cualquier \(c\in {\Bbb R}\backslash \{0\}\).
Aplicando este lema obtenemos
\[\max_{\bm{a}\in{\Bbb R}^d}\frac{n\left(\bm{a}^\prime{}\left(\overline{\bm{x}}-\bm{\mu}\right)\right)^2}{\bm{a}^\prime{}\bm{S_c}\bm{a}} =n\left(\overline{\bm{x}}-\bm{\mu}\right)^\prime{}\bm {S_c}^{-1}\left(\overline{\bm{x}}-\bm{\mu}\right)\in \Gamma^2(d,n-1).\] De este resultado se puede extraer el valor de \(c\) y finalmente se obtienen los que se conocen como intervalos de confianza simultáneos por el método de Scheffé:
\[\left(\ \bm{a}^\prime{}\overline{\bm{x}} - \sqrt{\frac{d(n-1)}{n-d}f_{d,n-d,\alpha}}\frac{\sqrt{\bm{a}^\prime{}\bm{S_c}\bm{a}}}{\sqrt{n}}\ , \bm{a}^\prime{}\overline{\bm{x}} + \sqrt{\frac{d(n-1)}{n-d}f_{d,n-d,\alpha}}\frac{\sqrt{\bm{a}^\prime{}\bm {S_c}\bm{a}}}{\sqrt{n}}\ \right)\]
o equivalentemente
\[\left(\ \bm{a}^\prime{}\overline{\bm{x}} - \sqrt{\frac{d}{n-d}f_{d,n-d,\alpha}\bm{a}^\prime{}\bm{S}\bm{a}}\ , \bm{a}^\prime{}\overline{\bm{x}} + \sqrt{\frac{d}{n-d}f_{d,n-d,\alpha}\bm{a}^\prime{}\bm{S}\bm{a}}\ \right)\]
Observación. Se puede demostrar que los intervalos de confianza simultáneos por el método de Scheffé coinciden con la proyección de la elipse de confianza sobre cada una de las direcciones determinadas por los vectores \(\bm{a}\). En concreto, si en \(\bm{a}\) se consideran las direcciones de los ejes, se obtendrían intervalos de confianza para cada componente.
La tabla siguiente permite comparar los valores de \(c\) para el cálculo de los intervalos de confianza, extraídos de la \(t\) de Student frente a los que se obtienen mediante el método de Scheffé.
| \(\sqrt{\frac{d(n-1)}{n-d}f_{d,n-d,0.05}}\) | |||
| \(n\) | \(t_{n-1,0.025}\) | \(d=4\) | \(d=10\) |
| 15 | 2.145 | 4.14 | 11.52 |
| 25 | 2.064 | 3.60 | 6.39 |
| 50 | 2.010 | 3.31 | 5.05 |
| 100 | 1.970 | 3.19 | 4.61 |
| \(\infty\) | 1.960 | 3.08 | 4.28 |
2.4.4 Intervalos de confianza simultáneos por el método de Bonferroni
Otro método para obtener intervalos de confianza simultáneos es el método de Bonferroni. Es una alternativa válida en cualquier contexto en el que se requiera una cantidad finita de intervalos simultáneos, ya que no se basa en la naturaleza probabilística del problema en cuestión (como sí lo hace el método de Scheffé), sino que su fundamento radica simplemente en la subaditividad de la probabilidad.
Si \(C_1,\ldots,C_m\) consisten en los sucesos respectivos de que cada intervalo de confianza contenga al parámetro correspondiente,
\[\begin{aligned} P(C_i\ \mbox{cierto}\ \forall i) &= 1-P(C_i\ \mbox{falso para algún}\ i) \\ &\geq 1-\sum_{i=1}^m P(C_i\ \mbox{falso})=1-\left(\alpha_1+\cdots +\alpha_m\right)\end{aligned}\]
siendo \(1-\alpha_1,\ldots,1-\alpha_m\) los niveles de confianza individuales de cada intervalo. Así, para alcanzar un nivel de confianza simultáneo \(1-\alpha\) basta con tomar \(\alpha_1,\ldots,\alpha_m\) de modo que \(\alpha_1+\cdots+\alpha_m=\alpha\), por ejemplo mediante \(\alpha_1=\cdots=\alpha_m=\alpha/m\).
La tabla siguiente muestra el cociente de longitudes (para \(1-\alpha=0.95\)), cuando se construyen intervalos para cada componente:
\[\frac{\mbox{Longitud del intervalo de Bonferroni}} {\mbox{Longitud del intervalo de Scheffé}} =\frac{t_{n-1,\alpha/(2m)}}{\sqrt{\frac{d(n-1)}{n-d}f_{d,n-d,\alpha}}}.\]
| \(m=d\) | |||
| \(n\) | 2 | 4 | 10 |
| 15 | 0.88 | 0.69 | 0.29 |
| 25 | 0.90 | 0.75 | 0.48 |
| 50 | 0.91 | 0.78 | 0.58 |
| 100 | 0.91 | 0.80 | 0.62 |
| \(\infty\) | 0.91 | 0.81 | 0.66 |
Ejemplo. Sobre el ejemplo de las puntuaciones de tests de inteligencia, vamos a calcular los intervalos de confianza para la calificación media del test 1 y del test 2, al nivel de confianza del 95%, obtenidos de manera individual, y simultáneos por el método de Scheffé y por el método de Bonferroni. Así, en la Figura 2.7 se representan mediante una elipse en color rojo la región de confianza para el vector de medias \(\bm{\mu}=(\bm{\mu_1}, \bm{\mu_2})^\prime{}\). En el centro de la elipse se sitúa el vector con las medias muestrales \(\overline{\bm{x}}=(102, 98)^\prime{}\).
Al proyectar la elipse sobre los ejes horizontal y vertical se obtienen los intervalos representados en color verde, que serían intervalos de confianza simultáneos por el método de Scheffé. Los intervalos de confianza simultáneos por el método de Bonferroni vienen representados en color negro. Como cabía esperar, son más pequeños que los intervalos simultáneos por el método de Scheffé. Por último, los intervalos de confianza individuales han sido representados con trazo azul. Son los más pequeños, también conforme a lo previsible.
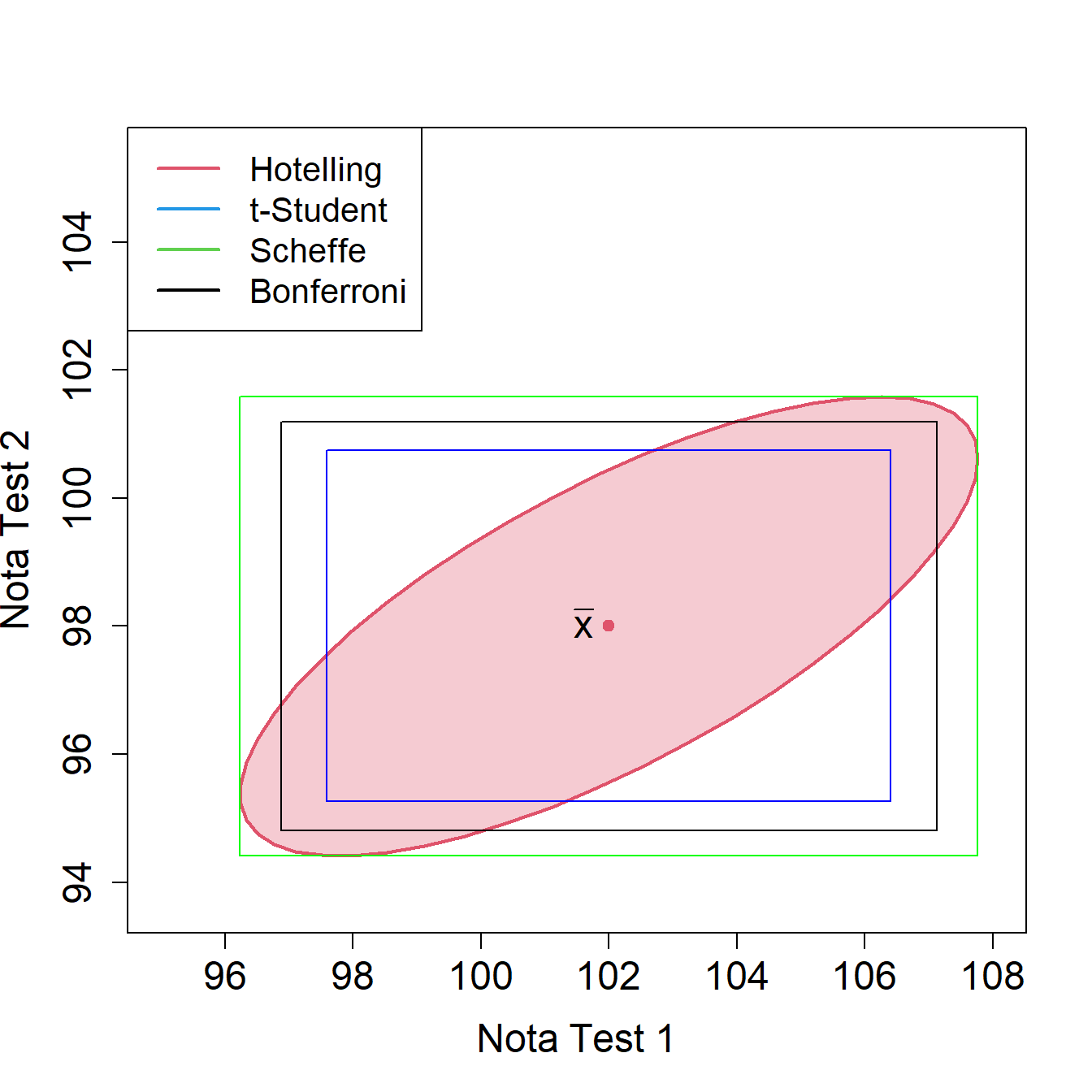
Figura 2.7: Región de confianza para el vector de medias (elipse), junto con intervalos de confianza individuales (trazo azul), simultáneos por el método de Bonferroni (trazo negro) y simultáneos por el método de Scheffé (trazo verde).