Other publications: Geostatistical Analysis of Functional Data
Este trabajo es fruto del proyecto fin de máster, Máster en Técnicas Estadísticas, dirigido por el profesor Manuel Febrero Bande. Defendido el 27-01-2011
Resumen:
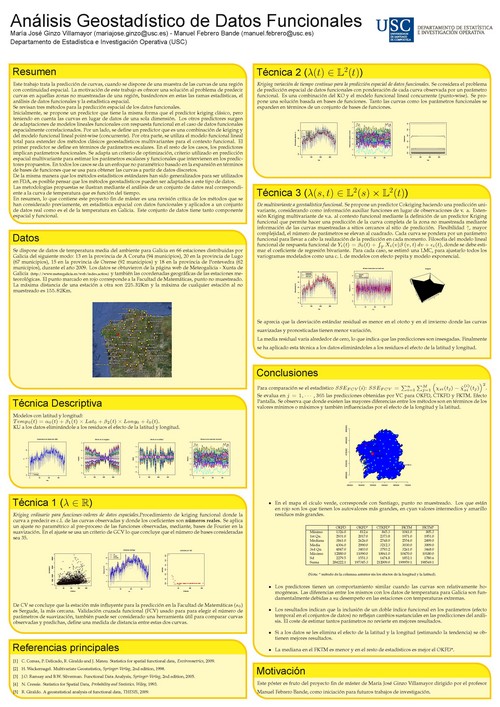
El análisis de datos funcional se ocupa de la modelización estadística de variables aleatorias que toman valores en un espacio de funciones (variables funcionales). Varias técnicas estadísticas estándares tales como la regresión, ANOVA o componentes principales, entre otros, han sido considerados desde el punto de vista funcional. En general, estas metodologías se centran en variables funcionales independientes e idénticamente distribuidas. Sin embargo, en varias disciplinas de las ciencias aplicadas, existe un gran interés en la modelización de datos funcionales espacialmente correlados. En particular, la mayoría de ellos están interesados en el modelado de datos funcionales espacialmente correlacionados. Este es el tema aquí tratado. En concreto, este proyecto trata la predicción de curvas, cuando se dispone de una muestra de las curvas de una región con continuidad espacial. Se revisan tres métodos para la predicción espacial de los datos funcionales. Inicialmente, se propone un predictor que tiene la misma forma que el predictor kriging clásico, pero teniendo en cuenta las curvas en lugar de datos de una sola dimensión. Los otros predictores surgen de adaptaciones de modelos lineales funcionales con respuesta funcional en el caso de datos funcionales espacialmente correlacionados. Por un lado, se define un predictor que es una combinación de kriging y del modelo funcional lineal point-wise (concurrente). Por otra parte, se utiliza el modelo funcional lineal total para extender dos métodos clásicos geoestadísticos multivariantes para el contexto funcional. El primer predictor se define en términos de parámetros escalares. En el resto de los casos, los predictores implican parámetros funcionales. Se adapta un criterio de optimización, criterio utilizado en predicción espacial multivariante para estimar los parámetros escalares y funcionales que intervienen en los predictores propuestos. En todos los casos se da un enfoque no paramétrico basado en la expansión en términos de bases de funciones que se usa para obtener las curvas a partir de datos discretos. Las metodologías propuestas se ilustran mediante el análisis de un conjunto de datos real correspondiente a la curva de temperatura que es función del tiempo.
Más información del proyecto:
© Mª José Ginzo Villamayor. All Rights Reserved. Designed by mariajose.ginzo@usc.es
